گاهی شما شبکه عصبی مدنظرتان را ساخته اید و می بینید که روی مجموعه آموزشی به خوبی عمل می کند، اما به اندازه کافی روی مجموعه آزمایشی خوب عمل نمی کند. این موضوع نشان دهنده مسئله بیش برازش داده ( Overfitting ) می باشد و یعنی شبکه عصبی شما واریانس بسیار زیادی دارد و نمی تواند با دادهای که هنوز مورد آموزش قرار نگرفته همخوانی داشته باشد.
دو روش رایج برای حل این مسئله وجود دارد که در ادامه توضیحی کوتاه از آن ها مطرح خواهیم کرد:
- دریافت داده های بیشتر
- استفاده از نظم دهی ( Regularization )
عمل دریافت میزان بیشتری داده تقریباً یک امر غیرممکن است و در عین حال بسیار هزینه بر می باشد. بنابراین، نظم دهی یک روش معمول برای کاهش بیش برازش می باشد و به مرور زمان کارآیی مدل را نیز بهبود می بخشد.
در این مقاله، الگوریتم های L2 Regularization و Dropout، به عنوان روش های نظم دهی در شبکه های عصبی، معرفی می شوند. سپس کد مربوط به هر کدام از آن ها را ارائه خواهیم کرد و تأثیر آن ها روی کارآیی شبکه عصبی قابل رویت خواهد بود.

L2 Regularization
در یادگیری عمیق هدف کلی به حداقل رسانی تابع هزینه ( در مقاله های گذشته توضیح داده شده است )زیر می باشد:
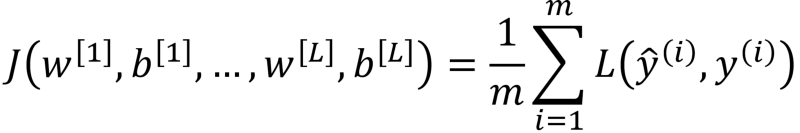
جایی که L می تواند هر تابع هزینه ای باشد ( مانند تابع Cross-entropy ). حال، برای L2 Regularization پارامتری به منظور تنظیم وزن ها اضافه می شود و معادله زیر حاصل خواهد شد:
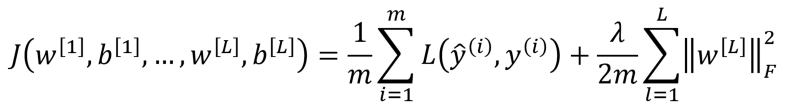
جایی که 𝜆 ( لاندا ) پارامتر نظم دهی می باشد. F به عنوان پارامتر نرمال Frobenius شناخته می شود و درواقع برابر با مجذور نرمال یک ماتریس می باشد.
لاندا پارامتری است که وابسته به شرایط می تواند تنظیم شود یعنی مقدار بالای وزن ها با درنظر گرفتن مقدار بالایی برای لاندا قابل کنترل خواهد بود و بطور مشابه مقدار کم برای لاندا به منظور تنظیم مقدار کم وزن ها درنظر گرفته می شود. از آنجایی که تابع هزینه باید حداقل رسانی شود، تناسب مطرح شده منطقی به نظر می رسد و با اضافه کردن مجذور نرمال ماتریس وزن ها و ضرب آن در پارامتر نظم دهی، وزن های زیاد به نوعی تنظیم می شود و تابع هزینه کاهش می یابد.
چرا Regularization مفید است؟
همانظور که گفته شد، اضافه کردن پارامتر نظم دهی، مقادیر درون ماتریس وزن را کاهش خواهد داد و این موضوع شبکه عصبی را ناهمبند می کند. تابع فعال سازی ( در مقاله های گذشته توضیح داده شده است )، از طریق رابطه زیر برای جمع وزن ها مطرح می شود:
با کاهش مقادیر ماتریس وزن، z نیز کاهش می یابد، که در پی آن تأثیر تابع فعال سازی نیز کاهش می یابد. بنابراین، یک تابع با پیچیدگی کمتر، به نسبت همخوانی بیشتری با داده ها خواهد داشت و بطور مؤثرتری بیش برازش را کاهش می دهد.
Dropout Regularization
این مدل، همه لایه های یک شبکه عصبی را می پیماید و احتمالی برای حفظ یا حذف نودها در نظر می گیرد. البته لایه ورودی و خروجی بطور مشابه حالت اولیه حفظ می شوند. احتمال حفظ هر نود به صورت تصادفی تعیین می شود و ما فقط آستانه ای برای آن درنظر می گیریم، مقداری که مشخص کند نود حفظ شده یا خیر.
به عنوان مثال، اگر مقدار آستانه را ۰٫۷ درنظر بگیرید، احتمال حذف نود از شبکه، برابر ۳۰٪ خواهد بود. بنابراین این موضوع منجر به پیدایش شبکه های عصبی کوچکتری مانند شکل زیر می شود.
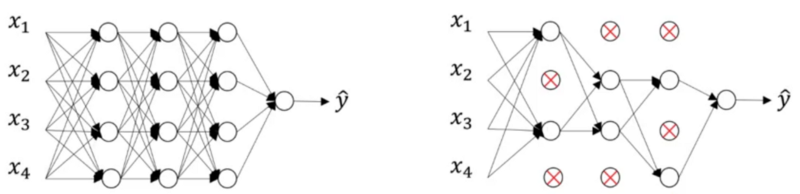
چرا dropout مفید است؟
ممکن است به نظر برسد حذف تصادفی نودها از شبکه عصبی برای نظم دهی به آن، امری به دور از منطق است اما با این حال نیز Dropout، یک روش بسیار محبوب و کاملاً تأیید شده در زمینه کارآیی شبکه های عصبی می باشد. حال چرا این مدل به خوبی عمل می کند؟
Dropout درواقع به این معنی است که یک شبکه عصبی نمی تواند به یک نود ورودی متکی باشد، چراکه هر کدام از آن ها احتمالی تصادفی برای حذف شدن دارند. بنابراین یک شبکه عصبی تمایلی برای اختصاص وزن بالا به ویژگی های اصلی ندارد، چراکه امکان حذف آن ها نیز وجود دارد. در پی این موضوع، وزن ها در میان تمام ویژگی ها تقسیم می شود و مقادیر کمتری برای آن ها درنظر گرفته می شود و این امر تأثیر بسزایی در نظم دهی و یکدست شدنِ مدل دارد.
پیاده سازی Regularization
حال، پیاده سازی دو الگوریتم Dropout و L2 Regularization را روی چند نمونه داده ارائه می کنیم تا تأثیرات آن ها روی کارآیی شبکه عصبی مشخص شود.
ایجاد یک نمونه مجموعه داده
پیاده سازی را با ایجاد یک نمونه مجموعه داده آغاز کرده و پس از وارد کردن کتابخانه های ضروری مدنظر، قطعه کد زیر را اجرا می کنیم:

شکل زیر حاصل می شود:
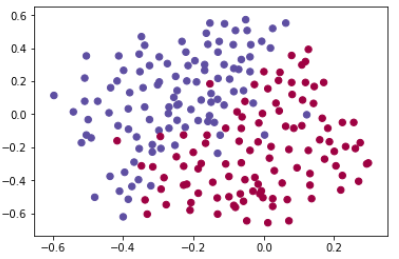
بسیارخوب، این یک نمونه مجموعه داده تصادفی با دو کلاس است، حال می خواهیم یک شبکه عصبی بنویسیم که هرکدام از این داده ها را دسته بندی کند و یک محدوده تصمیم گیری ایجاد کند.
مدل Non-regularized
کدی برای پیاده سازی این مدل از Regularization:
def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):
grads = {}
costs = []
m = X.shape[1]
layers_dims = [X.shape[0], 20, 3, 1]
# Initialize parameters dictionary.
parameters = initialize_parameters(layers_dims)
# Gradient descent
for i in range(0, num_iterations):
# Forward propagation
if keep_prob == 1:
a3, cache = forward_propagation(X, parameters)
elif keep_prob < 1:
a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)
# Cost function
if lambd == 0:
cost = compute_cost(a3, Y)
else:
cost = compute_cost_with_regularization(a3, Y, parameters, lambd)
# Backward propagation.
assert(lambd == 0 or keep_prob == 1)
if lambd == 0 and keep_prob == 1:
grads = backward_propagation(X, Y, cache)
elif lambd != 0:
grads = backward_propagation_with_regularization(X, Y, cache, lambd)
elif keep_prob < 1:
grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)
# Update parameters.
parameters = update_parameters(parameters, grads, learning_rate)
# Print the loss every 10000 iterations
if print_cost and i % 10000 == 0:
print("Cost after iteration {}: {}".format(i, cost))
if print_cost and i % 1000 == 0:
costs.append(cost)
# plot the cost
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('iterations (x1,000)')
plt.title("Learning rate =" + str(learning_rate))plt.show() return parameters
برای درک بهتر کد بالا لازم است زمان قابل توجهی درنظر بگیرید، دقت داشته باشید که متغیر lambd برای الگوریتم L2 Regularization مفید است. همچنین متغیر keep_prob نیز برای الگوریتم Dropout مفید می باشد.
حال با دستورهای زیر، یک شبکه عصبی را بدون Regularization اجرا می کنیم و خروجی ( دقت ) آن را به عنوان کارآیی پایه درنظر می گیریم:

خروجی حاصل:
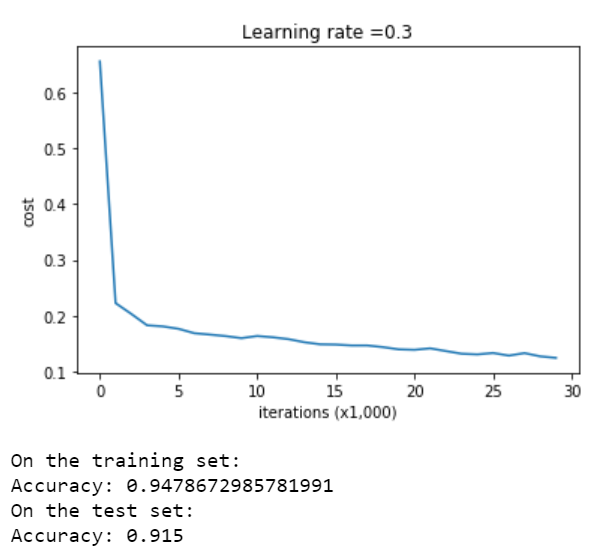
بد نبود، حال دستورهای زیر برای رسم نمودار آن اجرا می کنیم:
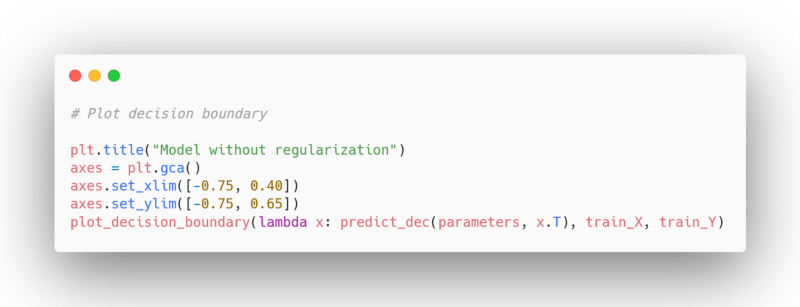
نمودار حاصل:
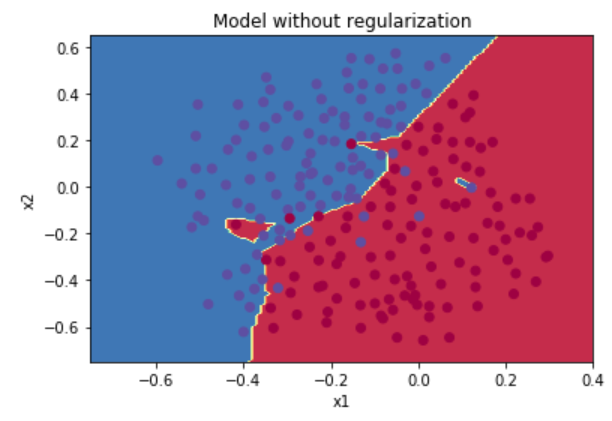
در نمودار بالا، مدل مد نظر در بعضی قسمت های داده دچار بیش برازش می باشد. از این مقادیر به عنوان میزان پایه ای خطا و کارآیی مدل در تشخیص مفید بودن Regularization، استفاده خواهیم کرد.
L2 Regularization
قبل از استفاده از L2 Regularization، لازم است که تابعی برای محاسبه هزینه Regularization، تعریف کنیم:

سپس، پس انتشار ( در مقاله های قبلی توضیح داده شد ) به همراه Regularization را تعریف می کنیم:

بسیار عالی، حال ما می توانیم از مدلمان به همراه L2 Regularization استفاده کنیم، متغیر lambda برابر ۰٫۷ درنظر گرفته می شود و خواهیم داشت:
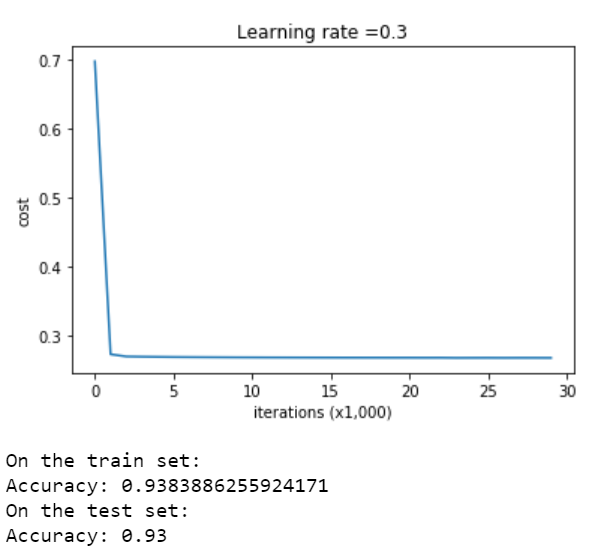
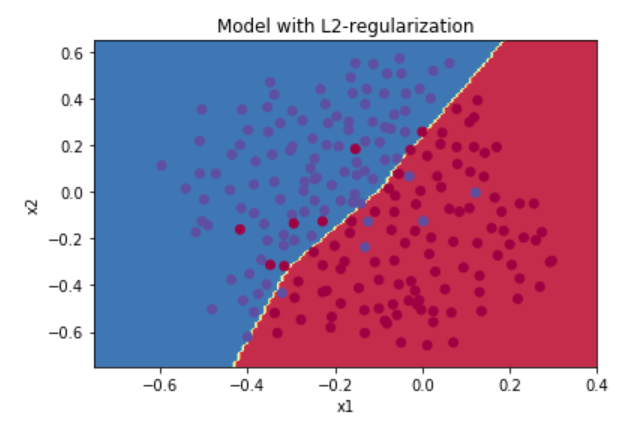
همانطور که مشاهده می شود، توانستیم به دقت مناسب روی مجموعه داده آزمایشی دستیابیم و دیگر بیش برازش داده نداشته باشیم.
حال ببینیم آیا Dropout می تواند بهتر از این مدل عمل کند یا خیر.
Dropout
در ابتدا لازم است پیش انتشار را تعریف کنیم چراکه می خواهیم اثر نود های اصلی به صورت تصادفی حذف شود:
def forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):
np.random.seed(1)
# Retrieve parameters
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
D1 = np.random.rand(A1.shape[0],A1.shape[1]) # Step 1: initialize matrix D1 = np.random.rand(..., ...)
D1 = D1<keep_prob # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)
A1 = np.multiply(D1, A1) # Step 3: shut down some neurons of A1
A1 = A1/keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
D2 = np.random.rand(A2.shape[0],A2.shape[1]) # Step 1: initialize matrix D2 = np.random.rand(..., ...)
D2 = D2<keep_prob # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)
A2 = np.multiply(D2, A2) # Step 3: shut down some neurons of A2
A2 = A2/keep_prob # Step 4: scale the value of neurons that haven't been shut down
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)
return A3, cache
حال باید پس انتشار را برای مدل Dropout تعریف کنیم:
def backward_propagation_with_dropout(X, Y, cache, keep_prob):
m = X.shape[1]
(Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = A3 - Y
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dA2 = np.multiply(dA2, D2) # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagation
dA2 = dA2/keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T)
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dA1 = np.multiply(dA1, D1) # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagation
dA1 = dA1/keep_prob # Step 2: Scale the value of neurons that haven't been shut down
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
"dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
بسیار عالی، حال ببینیم مدل مد نظر با Dropout و آستانه ۰٫۸ چگونه عمل خواهد کرد:
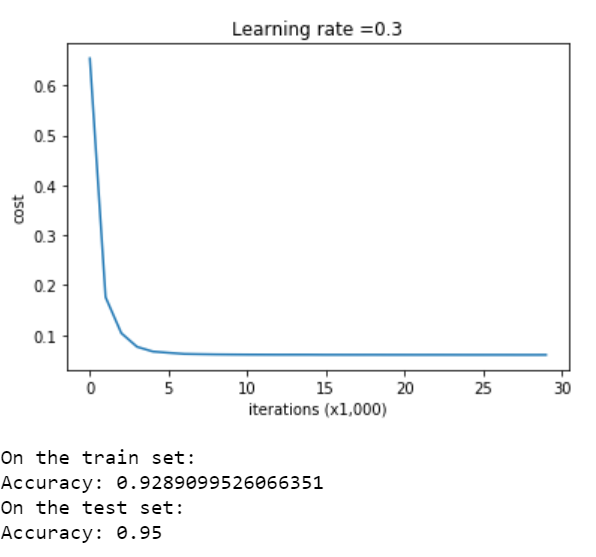
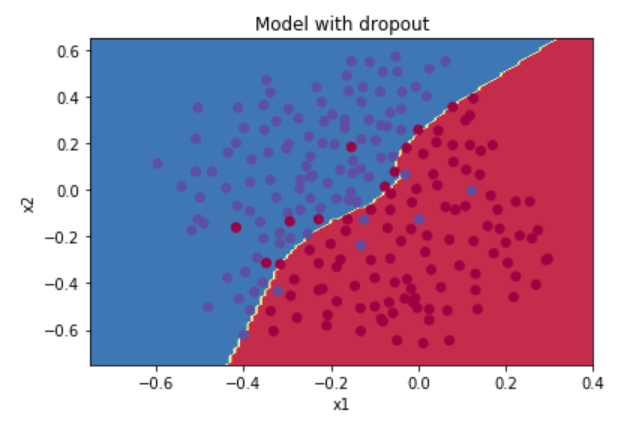
همانطور که مشاهده می فرمایید، با استفاده از Dropout توانستیم به دقتی بهتر از مدل قبل دست پیدا کنیم.
بسیارعالی، در این مقاله شما یاد گرفتید که چگونه Regularization می تواند کارآیی یک شبکه عصبی را بهبود دهد، و همچنین با پیاده سازی L2 Regularization و Dropout برای بهبود دسته بندی، آشنا شدید.
بیشتر بخوانید :
- هوش مصنوعی مولد تهدیدات جدیدی برای امنیت سایبری ایجاد می کند
- فناوری تشخیص پلاک خودرو چگونه جامعه را هوشمندتر می کند
- گوگل ساختار سازمانی خود را جهت تمرکز بر هوش مصنوعی اصلاح می کند
- پلاک خوان های شهر گرینزبوروی آمریکا فعلاً قرار نیست افزایش پیدا کنند
- فرماندار اوکلند از پلاک خوان ها حمایت می کند اما مخالفان در اثربخشی آن تردید دارند
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب




