GAN مخفف عبارت Generative Adversarial Networks به معنای شبکه های مولد تخاصمی است. از این پس از این عبارت مختصر شده بسیار استفاده خواهیم کرد.
در این آموزش به صورت قدم به قدم، ساختمان و استدلالی که منجر به GAN ها می شود را به شما توضیح می دهیم.
مقدمه
یان لکون ( Yann LeCun ) ایده ی GAN را به عنوان “جالب ترین ایده ی ۱۰ سال گذشته در یادگیری ماشین” توصیف کرده است. و البته چنین تعریفی اگر از چنین محقق برجسته ای در حوزه یادگیری عمیق حاصل شود ، یک تبلیغ و توصیف عالی برای موضوع مورد بحث ماست!
شبکه های مولد تخاصمی ( GAN ) که از سال ۲۰۱۴ توسط Ian J. Goodfellow و نویسندگانش در مقاله های شبکه های مولد تخاصمی معرفی شدند، تا کنون موفقیت های بزرگی داشته اند.
بسیار خب! شبکه های مولد تخاصمی چیست؟ چه چیزی آن ها را “جالب” می کند؟ در این پست خواهیم دید که آموزش تخاصمی یک ایده بسیار روشنگر است که در عین سادگی زیبا است ، نشان دهنده یک پیشرفت واقعی مفهومی برای یادگیری ماشین و مخصوصاً برای مدل های مولد است (مانند همان روش پس انتشار، یک ترفند ساده اما واقعاً هوشمندانه است که ایده اصلی شبکه های عصبی را بسیار محبوب و کارآمد کرد).
قبل از اینکه وارد جزئیات شویم بیاید مروری سریع داشته باشیم بر این که GAN ها برای چه چیزی ساخته شده اند.
GAN ها به دسته ی مدل های مولد ( Generative Models ) تعلق دارند. این بدان معناست که آن ها قادر به بسط دادن و یا تولید محتوای جدید هستند (خواهیم دید که چگونه). برای نشان دادن این مفهوم “مدل های مولد” ، می توانیم به چند نمونه معروف از نتایج به دست آمده با GAN ها نگاهی بیندازیم.

به طور طبیعی ، این توانایی در تولید داده های جدید باعث می شود که حداقل در نگاه اول GAN کمی جادویی به نظر برسد. در قسمت های بعدی ما بر روی جادوی ظاهری GAN ها صحبت خواهیم کرد تا به ایده ها ، ریاضیات و مدل سازی در پشت این مدل ها، پی ببریم. ما در ادامه نه تنها در مورد مفاهیم اساسی که GAN ها به آن ها تکیه می کنند بحث خواهیم کرد ، بلکه ، از همان ابتدا به صورت قدم به قدم استدلال هایی که منجر به این ایده ها می شود را بررسی خواهیم کرد.
بیشتر از این خودمان را درگیر نکنیم، بیائید GAN ها رو با یکدیگر دوباره کشف کنیم!
توجه: اگرچه ما سعی کردیم تا این مقاله را در حد امکان بدون نیاز به دانش قبلی بیان کنیم ، اما داشتن دانش اولیه قبلی در زمینه یادگیری ماشین لازم و اجتناب ناپذیر است. با این وجود ، بیشتر توضیحات لازم ذکر شده اند و برخی منابع لازم نیز ارائه می شود. ما واقعا سعی کردیم تا این مقاله تا حد ممکن صریح باشد تا خواندن آن راحت باشد. در بخش نظرات لطفا درج کنید که دوست دارید در مورد کدام بخش بیشتر مطالعه کنید. (در صورت امکان می توانید مقالات دیگر در مورد بخش های مختلف را به ما معرفی کنید).
نگاه کلی
در بخش اول ما درباره روند تولید متغیرهای تصادفی از توزیع داده شده بحث خواهیم کرد. سپس ، در بخش ۲ ، از طریق یک مثال نشان خواهیم داد که مسائلی که GAN ها برای حل آن تلاش می کنند ، می توانند به عنوان مسائل تولید متغیر تصادفی بیان شوند. در بخش ۳ ، ما در مورد شبکه های مولد مبتنی بر تطبیق صحبت خواهیم کرد و نحوه پاسخگویی آن ها به مسائل شرح داده شده در بخش ۲ را بیان خواهیم کرد. در آخر در بخش ۴ ، GAN ها را معرفی خواهیم کرد. به طور دقیق تر، ما معماری کلی آن ها را با تابع ضررشان ارائه خواهیم داد و تمام قسمت های قبلی را با یک دیگر پیوند خواهیم داد.
کلیت این مقاله تا حدی توسط فیلم کوتاه زیر نشان داده شده است:
تولید متغیر های تصادفی
در این بخش ، روند تولید متغیرهای تصادفی را مورد بحث قرار می دهیم: ما برخی از روش های موجود و به ویژه روش تبدیل معکوس را یادآوری می کنیم که امکان تولید متغیرهای تصادفی پیچیده را از متغیرهای تصادفی یکنواخت ساده، فراهم می کند. اگر چه این موضوعات کمی از موضوع اصلی ما یعنی GAN ها دور شود، اما در بخش بعدی پیوند عمیقی آن ها را با مدل های مولد ، خواهیم دید.
متغیرهای تصادفی یکنواخت می توانند شبه تصادفی تولید شوند
کامپیوتر ها اساساً قطعی هستند. (محاسبات آنها دقیق و بدون احتمال است.) بنابراین ، از نظر تئوری تولید عدد هایی که واقعاً تصادفی باشند، غیرممکن است (حتی اگر بتوانیم در مورد سوال ” تصادفی بودن، واقعا چیست؟” صحبت کنیم مسأله ای دشواری است). با این وجود می توان الگوریتم هایی را تعریف کرد که توالی ای از اعداد را تولید می کنند که خواص آن ها به خواص توالی اعداد تصادفی نظری بسیار نزدیک است. به طور دقیق تر ، کامپیوتر قادر است با استفاده از یک مولد عدد شبه تصادفی ، دنباله ای از اعداد را تولید کند که تقریباً از یک توزیع یکنواخت تصادفی بین ۰ تا ۱ پیروی می کند. توزیع یکنواخت یک روش بسیار ساده است که با انجام روش های مختلف بر روی آن می توان متغیرهای تصادفی پیچیده تری ساخت.
متغیرهای تصادفی که به عنوان نتیجه یک معادله یا یک فرآیند بیان شده اند
تکنیک های مختلفی وجود دارد که با هدف تولید متغیرهای تصادفی پیچیده تر انجام می شود. از جمله آن ها می توانیم روش تبدیل معکوس، نمونه برداری بازپس زننده ( Rejection Sampling ) ، الگوریتم متروپلیس-هیستینگز ( Metropolis-Hasting ) و … را بیابیم. همه این روش ها به ترفند های ریاضی مختلفی متکی هستند که عمدتاً در بازنمایی متغیر تصادفی که می خواهیم به عنوان نتیجه یک معادله (پیچیده تر از متغیرهای تصادفی ساده تر) یا یک فرآیند تولید شوند ، تشکیل شده است.
نمونه برداری بازپس زننده ، متغیر تصادفی را به عنوان نتیجه فرایندی بیان می کند که شامل یک توزیع پیچیده نیست، بلکه شامل نمونه گیری است که از یک توزیع ساده شناخته شده، انجام شده می شود و بسته به برخی شرایط ، مقدار نمونه را انتخاب یا رَد می کند. با تکرار این فرآیند تا زمانی که مقدار نمونه پذیرفته نشود ، می توانیم نشان دهیم که با شرط مناسب پذیرش، مقداری که به وسیله نمونه گیری انتخاب می شود ، از توزیع مناسبی پیروی می کند.
در الگوریتم Metropolis-Hasting ، ایده این است که یک زنجیره مارکوف ( Markov Chain ) یا به اختصار (MC) پیدا کنیم به گونه ای که توزیع ثابت این MC با توزیعی که می خواهیم از آن نمونه متغیرهای تصادفی خود را بدست آوریم ، مطابقت داشته باشد. پس از یافتن این MC ، ما می توانیم مسیری طولانی را بر روی این MC شبیه سازی کنیم تا بتوانیم بگوییم که به یک حالت پایدار رسیده ایم و سپس آخرین مقداری که از این راه بدست می آوریم را می توان از توزیع بهره در نظر گرفت.
ما دیگر به سراغ جزئیات نمونه برداری بازپس زننده و Metropolis-Hasting نخواهیم رفت چرا که این روش ها چیزی نیستند که ما را به سمت مفاهیم GAN ها سوق دهند (با این وجود ، کاربران علاقه مند می توانند مقالات و پیوند های ویکی پدیا را دنبال کنند). با این وجود، کمی بیشتر به روش تبدیل معکوس می پردازیم.
روش تبدیل معکوس
ایده روش تبدیل معکوس نشان دهنده ی مفهوم کلمه “پیچیده” است – در این مقاله “پیچیده” نه به صورت مفهوم ریاضی (مختلط) بلکه باید به معنای ” غیر ساده” درک شود؛ ما می دانیم چگونه می توان متغیر تصادفی را به عنوان نتیجه یک تابع اعمال شده بر روی متغیر تصادفی یکنواخت ، تولید کرد.
به مثال یک بعدی زیر توجه می کنیم. فرض کنید X یک متغیر تصادفی پیچیده باشد که می خواهیم از آن نمونه بگیریم و U یک متغیر تصادفی در بازه [۰,۱] است که می دانیم چگونه باید از آن نمونه بگیریم. یادآوری می کنیم که یک متغیر تصادفی کاملاً توسط تابع توزیع تجمعی ( CDF ) آن تعریف شده است. CDF یک متغیر تصادفی تابعی از حوزه تعریف متغیر تصادفی در بازه [۰,۱] است و در یک بعد تعریف می شود به گونه ای که:
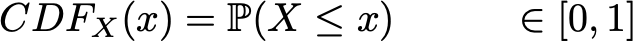
اما به طور کلی در مورد متغیر تصادفی U خواهیم داشت:
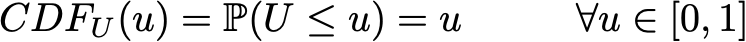
برای سادگی ، در اینجا فرض خواهیم کرد که تابع CDF_X معکوس پذیر است و معکوس آن مشخص شده است
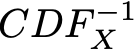
(این روش را می توان به سادگی برای موارد معکوس ناپذیر با تابع معکوس کلی نیز تعمیم داد ولی این موضوعی نیست که اینجا می خواهیم در مورد آن بحث کنیم.) پس اگر ما تعریف کنیم :
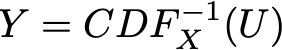
خواهیم داشت:
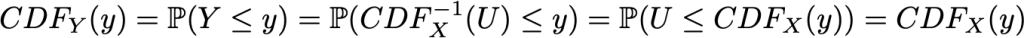
همانطور که می بینیم Y و X یک CDF یکسان دارند و پس متغیر تصادفی یکسانی را تعریف می کنند. بنابراین ، با تعریف Y به صورت بالا (به عنوان تابعی از یک متغیر تصادفی یکنواخت) موفق شده ایم تا یک متغیر تصادفی با توزیع هدفمند تعریف کنیم.
به طور خلاصه ، روش تبدیل معکوس روشی برای تولید یک متغیر تصادفی است که با تهیه یک متغیر تصادفی یکنواخت از طریق یک “تابع تبدیل” که به خوبی طراحی شده ( CDF معکوس ) می باشد، از توزیع معین پیروی می کند. این مفهوم “روش تبدیل معکوس” می تواند به مفهوم “روش تبدیل” که به طور کلی ، در تولید متغیرهای تصادفی به عنوان تابعی از برخی متغیرهای تصادفی ساده تر (که لزوماً یکنواخت نیست و بنابراین تابع تبدیل مفصل تر از معکوس CDF نیست) تشکیل می شود ، گسترش یابد. از نظر مفهومی ، هدف از “تابع تبدیل” تغییر شکل مجدد توزیع احتمال اولیه است: تابع تبدیل از جایی که توزیع اولیه نسبت به توزیع هدفمند خیلی زیاد باشد، مقادیر را گرفته و آن ها را در جایی که توزیع خیلی کم باشد، قرار می دهد.
مدل های مولد :
می خواهیم متغیرهای تصادفی بسیار پیچیده تولید کنیم …
فرض کنید می خواهیم تصاویر مربعی سیاه و سفید از سگ ها با اندازه n در n پیکسل تولید کنیم.
ما می توانیم هر داده را به صورت بردار N = nxn (با انباشت ستون ها در بالای یکدیگر) تغییر شکل دهیم به گونه ای که یک تصویر از سگ می تواند توسط یک بردار نمایش داده شود.(به عبارت دیگر ستون های ماتریس تصویر سگ را روی هم قرار داده تا یک بردار تشکیل شود.) و این بدین معنی نیست که تمام بردار ها را اگر دوباره به شکل مربعی برگردانیم دوباره شکل سگ ظاهر شود!
بنابراین ، ما می توانیم بگوییم که بردارهای N بعدی که بطور مؤثر چیزی ظاهری شبیه به سگ را شرح می دهند ، طبق توزیع احتمال بسیار خاص در کل فضای بردار N بعدی توزیع می شوند (برخی از قسمت های آن احتمال دارد سگ ها را نشان داده در حالی که برخی قسمت ها بعید است چنین چیزی را نشان دهند). به همین صورت، در این فضای بردار N بعدی ، توزیع احتمال برای تصاویر گربه ها ، پرندگان و غیره وجود دارد.
پس ، مسئله تولید یک تصویر جدید از سگ معادل مسئله تولید یک بردار جدید ذیل “توزیع احتمال سگ” در طول فضای بردار N بعدی است. بنابراین ، ما در حقیقت با تولید یک متغیر تصادفی با توجه به توزیع احتمال خاص روبرو هستیم.
در این مرحله می توان به دو نکته مهم اشاره کرد. اول “توزیع احتمال سگ” که گفتیم، توزیع بسیار پیچیده ای در فضایی بسیار بزرگ است. دوم ، حتی اگر بتوانیم وجود چنین توزیع اساسی را فرض کنیم (در واقع تصاویری وجود دارد که به نظر می رسد شبیه سگ و یا چیزهای دیگر هستند ولی اینگونه نیست) ، ما مشخصا نمی دانیم که چگونه می خواهیم به طور صریح، این توزیع را بیان کنیم. هر دو نکته قبلی، فرایند تولید متغیر های تصادفی از این توزیع را بسیار دشوار می کند. در ادامه می خواهیم سعی کنیم این دو مشکل را برطرف کنیم.
… پس اجازه دهید از روش تبدیل به وسیله ی یک شبکه عصبی به عنوان تابع استفاده کنیم!
اولین مشکل ما هنگام تولید تصویر جدید سگ این است که “توزیع احتمال سگ” در فضای بردار N بعدی یک مسئله بسیار پیچیده است و ما نمی دانیم چگونه مستقیماً متغیرهای تصادفی پیچیده تولید کنیم.
با این حال ، از آنجا که ما به خوبی می دانیم که چگونه N متغیر تصادفی یکنواخت غیر همبسته تولید کنیم ، می توانیم از این روش تبدیل استفاده کنیم. برای انجام این کار ، ما باید متغیر تصادفی N بعدی خود را به صورت حاصل یک تابع بسیار پیچیده اعمال شده بر یک متغیر تصادفی ساده N بعدی بیان کنیم!
در اینجا ، ما می توانیم تأکید کنیم که یافتن تابع تبدیل به این سادگی ها هم نیست؛ مانند گرفتن معکوس از تابع توزیع تجمعی به صورت بسته و غیر قابل تجزیه تحلیل (که آن را نمی دانیم) همانطور که در توصیف روش تبدیل معکوس انجام داده ایم. تابع تبدیل نمی تواند صریحاً بیان شود و بنابراین ، ما باید آن را از داده ها یادبگیریم.
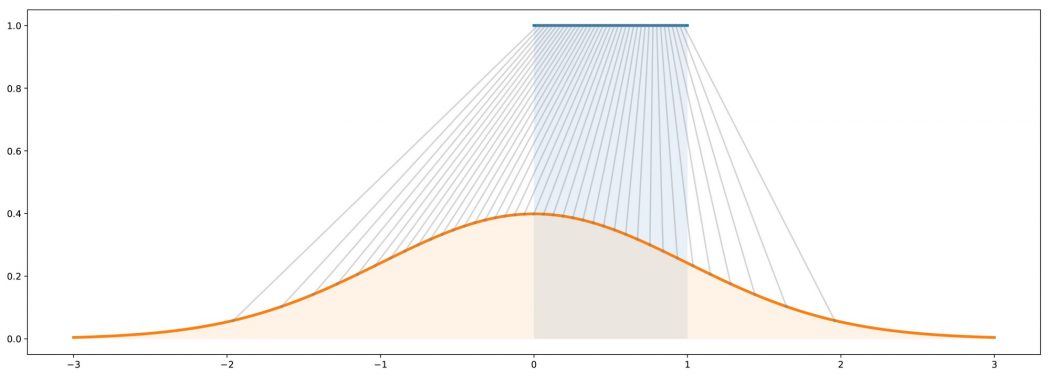
چون بیشتر اوقات در این موارد ، طبیعتا تابع بسیار پیچیده ای مدل سازی شبکه عصبی را نشان می دهد. بنابراین ، ایده این است که تابع تبدیل را توسط یک شبکه عصبی مدل سازی کنیم که به عنوان ورودی، یک متغیر تصادفی یکنواخت N بعدی را می گیرد و پس از آموزش، به عنوان خروجی متغیر تصادفی N بعدی می دهد که باید شبیه به “توزیع احتمال سگ” است. پس از طراحی معماری شبکه ، ما هنوز نیاز داریم آن را آموزش دهیم. در دو بخش بعدی ، ما در مورد دو روش هایی برای آموزش این شبکه های مولد صحبت خواهیم کرد ، همچنین ایده آموزش تخاصمی GAN ها!
شبکه های مولد تطبیق دهنده
سلب مسئولیت: نامگذاری “شبکه های مولد تطبیق دهنده” یک نام گذاری استاندارد نیست. با این حال ، می توانید برای بیان تحت اللفظی تر از “شبکه های مولد تطبیق دهنده ی لحظه ای” یا “شبکه های مولد تطبیق دهنده ی ویژگی ها” استفاده کنیم. ما فقط می خواهیم برای آنچه که در ادامه توصیف می کنیم از یک نام گذاری کلی تر استفاده کنیم.
آموزش مدل های مولد
تاکنون ، نشان داده ایم که مساله ما برای تولید یک تصویر جدید از سگ را می توان به مساله ایجاد یک بردار تصادفی در فضای بردار N بعدی که دنباله “توزیع احتمال سگ” است ، تبدیل کرد و ما پیشنهاد کردیم از یک روش تبدیل با استفاده از یک یک شبکه عصبی برای مدل سازی تابع تبدیل استفاده کنیم.
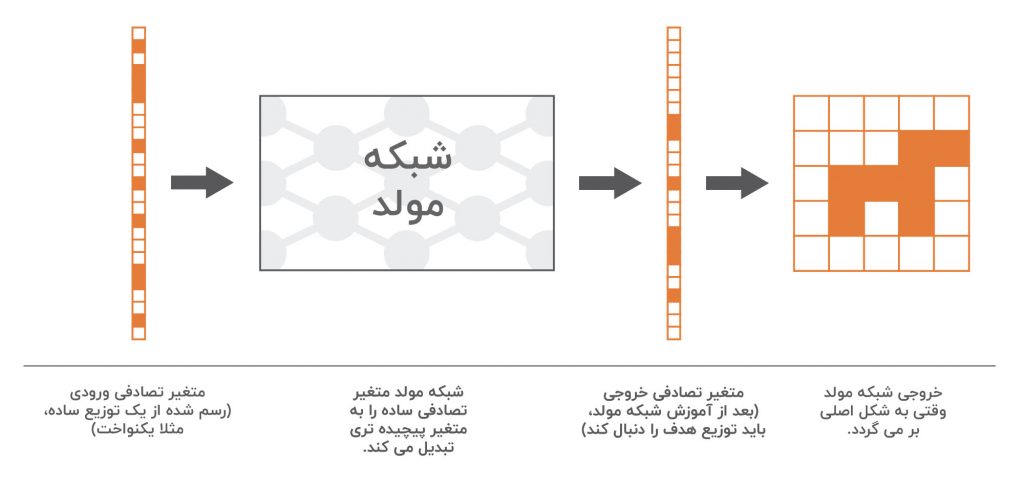
حال ، ما هنوز نیاز داریم تا شبکه را آموزش دهیم (بهینه سازی کنیم). برای این منظور می توانیم دو روش آموزش مختلف را پیشنهاد کنیم: یک روش مستقیم و غیر مستقیم. روش آموزش مستقیم شامل مقایسه توزیع واقعی و تولید توزیع احتمال و پس انتشار دادن ( خطا ) در شبکه است. این ایده ای است که بر شبکه های مولد تطبیق دهنده ( GMNs ) حاکم است. برای روش آموزش غیر مستقیم ، ما توزیع های واقعی و تولید شده را به طور مستقیم مقایسه نمی کنیم. درعوض ، شبکه ی مولد را آموزش می دهیم که این دو توزیع را از یک پروسه ی انحرافی عبور دهد به طوری که فرآیند بهینه سازی شبکه مولد با توجه به پروسه ی انحرافی ، توزیع تولید شده را به توزیع واقعی نزدیک می کند. این ایده آخر ایده ای است که در پشت شبکه های مولد تخاصمی ( GAN ) وجود دارد که در بخش بعدی ارائه خواهیم کرد. اما در حال حاضر ، بیایید با روش مستقیم و GMN ها شروع کنیم.
مقایسه دو توزیع احتمال براساس نمونه ها
همانطور که گفته شد ، ایده GMN ها آموزش شبکه مولد با مقایسه مستقیم توزیع تولید شده با شبکه واقعی است. با این حال ، ما نمی دانیم چگونه به طور صریح “توزیع احتمال سگ” را بیان کنیم و همچنین می توانیم بگوییم که توزیع تولید شده برای بیان صریح بسیار پیچیده است. بنابراین ، مقایسه بر اساس اصطلاحات صریح امکان پذیر نیست. اما اگر راهی برای مقایسه توزیع احتمال براساس نمونه ها داشته باشیم ، می توانیم از آن برای آموزش شبکه استفاده کنیم. در واقع ، ما یک نمونه از داده های واقعی داریم و می توانیم ، در هر تکرار روند آموزش ، نمونه ای از داده های تولید شده را ایجاد کنیم.
اگرچه ، در تئوری ، از هر فاصله (یا اندازه گیری شباهت) می توان برای مقایسه ی دو توزیع بر اساس نمونه ها استفاده کرد ، می توانیم رویکرد حداکثر میانگین اختلاف ( MMD ) را ذکر کنیم. MMD فاصله ای بین دو توزیع احتمال را تعیین می کند که می توان براساس نمونه های این توزیع ها محاسبه کرد. اگرچه این موضوع کاملاً خارج از محدوده این مقاله نیست ، اما ما تصمیم گرفته ایم که زمان بیشتری را به توصیف MMD اختصاص ندهیم. خواننده ای که می خواهد اطلاعات بیشتری درباره MMD کسب کند می تواند به این اسلاید ها ، این مقاله یا این مقاله مراجعه کند.
پس انتشار خطای تطبیق توزیع
بنابراین ، هنگامی که ما یک روش برای مقایسه دو توزیع بر اساس نمونه ها تعریف کردیم ، می توانیم روند آموزش شبکه مولد را در GMN تعریف کنیم. با توجه به متغیر تصادفی با توزیع احتمال یکنواخت به عنوان ورودی ، می خواهیم توزیع احتمال تولید شده در خروجی “توزیع احتمال سگ” باشد. ایده GMN ها سپس به صورت تکرار مراحل زیر شبکه را بهینه سازی خواهد کرد:
- تعدادی ورودی یکنواخت تولید کنید
- این ورودی ها را به شبکه وارد کرده و خروجی های تولید شده را جمع آوری کنید
- “توزیع احتمال سگ” واقعی و تولید شده را بر اساس نمونه های موجود مقایسه کنید (به عنوان مثال فاصله MMD بین نمونه تصاویر سگ واقعی و نمونه نمونه های تولید شده را محاسبه کنید)
- از پس انتشار برای ایجاد یک گرایدان نزولی برای کاهش فاصله (به عنوان مثال MMD) بین توزیع های واقعی و تولید شده استفاده کنید.
همانطور که در بالا نوشته شد ، هنگام دنبال کردن این مراحل ، ما از یک گرادیان نزولی بر روی شبکه با یک تابع ضرر ( Loss Function ) استفاده می کنیم که فاصله بین توزیع های واقعی و تولید شده در تکرار فعلی است.
شبکه های مولد تخاصمی
روش آموزش “غیر مستقیم”
رویکرد “مستقیم” ارائه شده در بالا ، مستقیماً توزیع تولید شده را با روش واقعی هنگام آموزش شبکه تولید مقایسه می کند. ایده درخشانی که بر GAN ها حاکم است این است که این مقایسه مستقیم را با یک غیرمستقیم جایگزین کند که به شکل پروسه ای انحرافی از این دو توزیع شکل بگیرد. سپس آموزش شبکه مولد با توجه به این پروسه به گونه ای که توزیع تولید شده را مجبور می کند تا به توزیع واقعی نزدیک تر و نزدیک شود، انجام می شود.
پروسه ی انحرافی GAN ها، اعمال یک تمایز بین نمونه های واقعی و تولید شده است. یا می توانیم پروسه “عدم تمایز” بگوییم زیرا می خواهیم تمایز تا حد ممکن شکست بخورد . بنابراین ، در یک معماری GAN ، یک متمایز کننده داریم ، نمونه هایی از داده های واقعی و تولید شده را می گیریم و سعی می کنیم آن ها را به بهترین وجه ممکن کلاسه بندی کنیم ، و یک مولد که آموزش دیده تا حد ممکن متمایز کننده را فریب دهد. بیایید با یک مثال ساده ببینیم که چرا رویکرد های مستقیم و غیرمستقیم که گفتیم باید از نظر تئوری به یک مولد بهینه یکسان منتهی شوند.
حالت ایده آل: مولد و متمایز کننده ی بی نقص
به منظور درک بهتر ” چرا آموزش مولد برای فریب یک متمایز کننده منجر به همان نتیجه ی آموزش مستقیم مولد برای مطابقت با توزیع هدف می شود؟” ، بیایید یک مثال ساده یک بعدی را در نظر بگیریم. فعلاً فراموش می کنیم که چگونه مولد و متمایز نمایش داده می شوند و آن ها را به عنوان مفاهیم انتزاعی در نظر می گیریم (که در زیر بخش مشخص خواهد شد). علاوه بر این ، هر دو مدل “بی نقص” در نظر گرفته می شوند (با ظرفیت های نامتناهی). به این معنا که توسط هیچ نوع مدل (پارامتری) محدود نمی شوند.
فرض کنید یک توزیع واقعی داریم ، مثلا یک گاوسی یک بعدی ، و ما یک مولد می خواهیم که از این توزیع احتمال نمونه برداری کند. سپس آنچه که ما آن را آموزش روش “مستقیم” نامیدیم ، به تنظیم مکرر مولد (تکرار گرادیان نزولی) برای” اصلاح تفاوت / خطای اندازه گیری شده” بین توزیع های واقعی و تولید شده می پردازد. سرانجام ، با فرض بی نقص بودن فرایند بهینه سازی ، باید به توزیع تولید شده ای برسیم که دقیقاً با توزیع واقعی مطابقت داشته باشد.
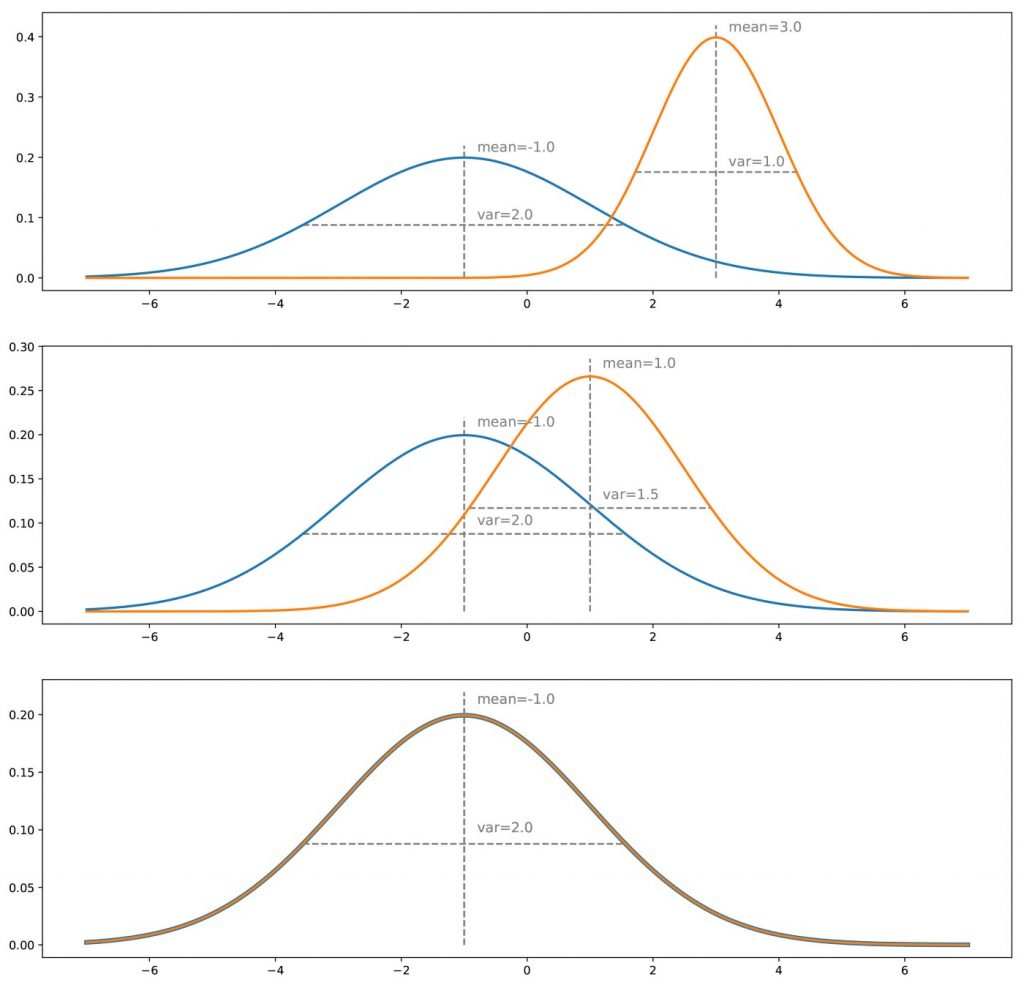
برای روش “غیر مستقیم” ، باید متمایز کننده را نیز در نظر بگیریم. فعلا فرض می کنیم متمایز کننده نوعی پیشگو است که دقیقا می داند توزیع واقعی و تولید شده چگونه هستند و با توجه به این اطلاعات، می تواند برای آن ها یک کلاس (“واقعی” یا “تولید شده”) تعیین کند. اگر این دو توزیع از یک دیگر فاصله ی زیادی داسشته باشند، متمایز کننده می تواند بیشتر نقاطی که به آن داده می شود را به راحتی و با سطح اطمینان بالا، کلاسه بندی کند. اگر می خواهیم متمایز کننده را فریب دهیم، باید توزیع های تولید شده را به توزیع های واقعی نزدیک کنیم. وقتی دو توزیع در تمام نقاط یکسان باشند، متمایز کننده سخت ترین شرایط را برای پیشبینی کلاس آن ها پیش رو دارد. به همین دلیل، برای هر نقطه احتمال “واقعی” یا “تولید شده” بودن یکسان خواهد بود و متمایز کننده تنها می تواند به طور شانسی یکی از دو مورد را درست پیشبینی کند.
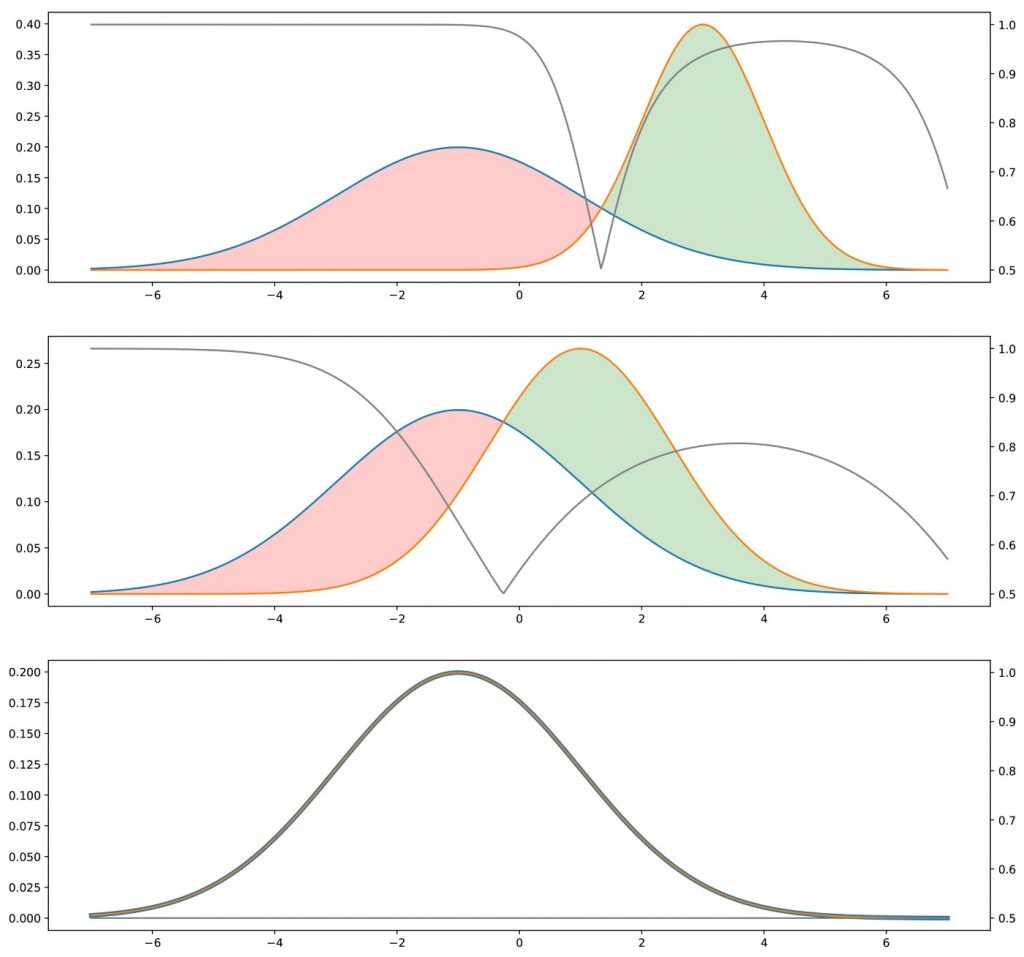
در اینجا، به نظر می رسد جای سوال دارد که آیا این روش غیرمستقیم ایده خوبی است یا خیر. در واقع ، به نظر می رسد این روش پیچیده تر است (ما باید مولد را بر اساس یک پروسه ی انحرافی به جای اینکه مستقیماً بر اساس توزیع ها بهینه کنیم) و به یک متمایز کننده نیاز داریم که ما اینجا آن را به عنوان پیشگویی معین در نظر می گیریم اما در واقعیت هیچ کدام بی نقص نیست. دشواری روش مقایسه مستقیم دو توزیع احتمال بر اساس نمونه ها نسبت به پیچیدگی آشکار روش غیرمستقیم ارجعیت دارد. برای نکته دوم ، بدیهی است که متمایز کننده شناخته شده نیست. با این وجود می توان آن را آموخت!
تقریب: شبکه های عصبی تخاصمی
حال بیایید حالت خاصی را که مولد و متمایز کننده معماری GAN ها را توصیف می کند شرح دهیم. مولد یک شبکه عصبی است که یک تابع تبدیل را مدل می کند. وقتی که آموزش دیده باشد، به عنوان ورودی یک متغیر تصادفی ساده گرفته و باید یک متغیر تصادفی که توزیع هدف را دنبال می کند را به عنوان خروجی برمی گرداند. با وجود این که بسیار پیچیده و ناشناخته است ، تصمیم گرفتیم مدل متمایز کننده را با شبکه عصبی دیگری مدل کنیم. این شبکه عصبی یک تابع متمایز کننده را مدل سازی می کند. به عنوان ورودی یک نقطه را می گیرد (در مثال سگ ما یک بردار N بعدی) و به عنوان خروجی احتمال “واقعی” بودن این نقطه را برمی گرداند.
توجه داشته باشید که این واقعیت که ما اکنون از یک مدل پارامتری را برای بیان مولد و متمایز کننده (به جای نسخه های ایده آل در زیرمجموعه قبلی) استفاده می کنیم ، در عمل تأثیر زیادی بر استدلال / شهود تئوری که در بالا آورده شده است ندارد: ما فقط به جای فضا های کامل ایده آل، در فضا های پارامتری کار می کنیم و بنابراین ، نقاط بهینه که باید در حالت ایده آل به آن برسیم می تواند با توجه به ظرفیت دقیق مدل های پارامتری “گرد” به نظر برسد.
پس از تعریف ، این دو شبکه می توانند به طور مشترک (همزمان) با اهداف مخالف آموزش داده شوند:
- هدف از مولد فریب متمایز کننده است ، بنابراین شبکه عصبی مولد آموزش داده شده است تا خطای کلاسه بندی نهایی (بین داده های واقعی و تولید شده) را به حداکثر برساند.
- هدف متمایز کننده این است که داده های تولید شده جعلی را کشف کنند ، بنابراین شبکه عصبی متمایز کننده آموزش دیده تا خطای کلاسه بندی نهایی را به حداقل برساند
بنابراین ، در هر تکرار از روند آموزش ، وزن شبکه مولد به منظور افزایش خطای کلاسه بندی (گرادیان صعودی خطا بر روی پارامترهای مولد) به روز می شود در حالی که وزن شبکه متمایز کننده برای کاهش این خطا ( گرادیان نزولی خطا بر پارامترهای متمایز کننده) به روز می شود.
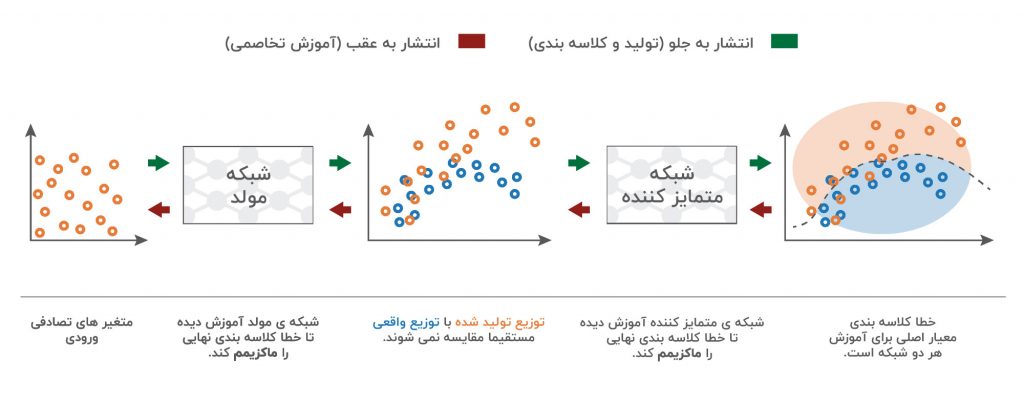
این اهداف متضاد و مفهوم ضمنی آموزش تخاصمی این دو شبکه ، دلیل نام “شبکه های تخاصمی” را توضیح می دهد: هر دو شبکه سعی می کنند یکدیگر را شکست دهند و با این کار ، هر دو بهتر و بهتر می شوند. رقابت بین آن ها باعث می شود این دو شبکه با توجه به اهداف مربوطه خود “پیشرفت” کنند. از نقطه نظر تئوری بازی ، حداقل می توانیم از این روش را به عنوان یک بازی دو نفره یاد کنیم که وضعیت تعادل با وضعیتی که مولد، داده ها را با توزیع هدفمند دقیق تولید می کند در حالی که که متمایز کننده، پیش بینی “واقعی” یا “تولید شده” بودن آن ها را با احتمال ½ انجام می دهد.
جزئیات ریاضی در مورد GAN ها
توجه: این بخش کمی فنی تر است و برای درک کلی GAN ها به طور کلی لازم نیست. بنابراین ، خوانندگانی که نمی خواهند در حال حاضر برخی از ریاضیات را بخوانند می توانند فعلاً از این بخش عبور کنند. برای سایرین ، ببینیم چگونه تئوری های گفته شده به صورت ریاضی در می آیند.
سلب مسئولیت: معادلاتی که در ادامه گفته شده از مقاله Ian Goodfellow نیست. در اینجا فرمول نویسی ریاضی دیگری را به دو دلیل پیشنهاد کردیم: اول اینکه کمی به تئوری هایی که در بالا گفته شد نزدیک تر باشد و دوم اینکه چون معادلات مقاله اصلی از ابتدا واضح هستند و بازنویسی دوباره آن ها مفید نیست . توجه کنید که ما کاملاً وارد ملاحظات عملی (محو شدگی گرادیان یا موارد دیگر) که مربوط به توابع ضرر مختلف است، نمی شویم. ما خواننده را به شدت تشویق می کنیم که به معادلات مقاله اصلی نیز نگاهی بیندازد: تفاوت اصلی در این است که Ian Goodfellow و دیگر نویسندگان به جای خطای مطلق (همانطور که در ادامه خواهید خواند) با خطای آنتروپی متقاطع کار کرده اند. علاوه بر این ، در ادامه ما یک مولد و متمایز کننده با ظرفیت های نامحدود در نظر می گیریم.
الگو سازی شبکه های عصبی در اصل نیاز به تعریف دو چیز دارد: یک معماری و یک تابع ضرر. ما قبلاً معماری شبکه های مولد تخاصمی را شرح داده ایم. این برنامه در دو شبکه تشکیل شده است:
- یک شبکه مولد (.)G که از ورودی تصادفی z با چگالی p_z استفاده می کند و خروجی x_g = G (z) را، که باید (پس از آموزش) دنبال کند، توزیع احتمال هدفمند را بر می گرداند.
- یک شبکه متمایز کننده (.)D که ورودی x را دریافت می کند که می تواند یک داده “واقعی” ( x_t باشد که چگالی آن به p_t نشان داده شده است) یا یک “تولید شده” ( x_g که چگالی آن p_g چگالی ناشی از چگالی p_z است و از طریق G تولید شده) و این احتمال D (x)، را به عنوان “واقعی” بودن داده ی x برمی گرداند.
حال اجازه دهید نگاهی دقیق تر به “تئوری” تابع ضرر GAN ها بیندازیم. اگر داده های “واقعی” و “تولید شده” را به همان نسبت ارسال کنیم ، خطای مطلق مورد انتظار از متمایز کننده می تواند به صورت زیر بیان شود:
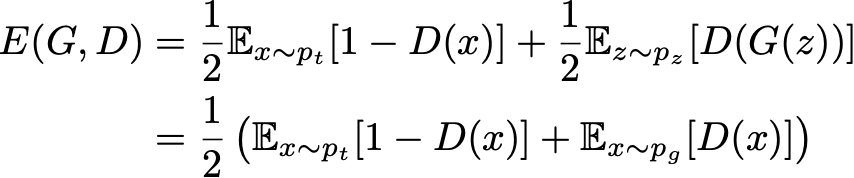
هدف مولد این است که متمایز کننده را که هدف آن، توانایی تفکیک داده های واقعی و تولید شده است، فریب دهد. بنابراین ، هنگام آموزش مولد ، می خواهیم این خطا را حداکثر کنیم در حالی که سعی می کنیم آن را برای متمایز کننده به حداقل برسانیم. این به ما می دهد:
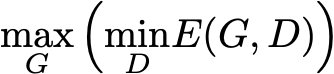
برای هر مولد G داده شده (همراه با القا چگالی احتمال p_g) ، بهترین متمایز کننده آن است که بتواند این تابع را مینیمم کند.
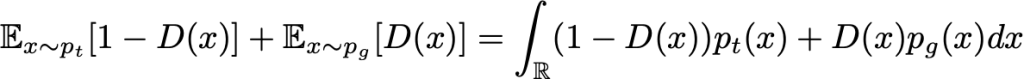
به منظور به مینیمم کردن (با توجه به D) این انتگرال ، ما می توانیم تابع داخل انتگرال را به ازای هر مقدار x ، مینیمم کنیم . به این ترتیب بهترین متمایز کننده ی ممکن برای مولد مشخص می شود.
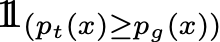
(در حقیقت ، یکی از بهترین ها ، زیرا مقدار x آنقدری است که p_t (x) = p_g (x)
به روش دیگری نیز به جواب برسد اما این در ادامه اهمیت ندارد ). سپس G را پیدا می کنیم که این تابع را ماکزیمم کند.
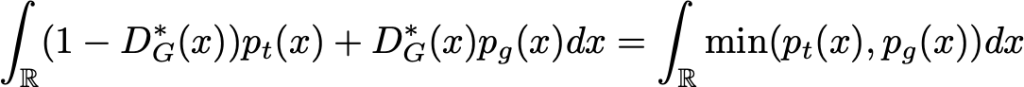
باز هم ، برای به حداکثر رساندن (با توجه به G) این انتگرال ، ما می توانیم تابع را برای هر مقدار x ، ماکزیمم کنیم. از آنجا که چگالی p_t مستقل از مولد G است ، ما نمی توانیم G به گونه ای بهتر از حالت زیر تنظیم کنیم:
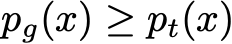
البته ، از آنجا که p_g یک چگالی احتمال است که باید به ۱ برسذ ، ما لزوماً برای بهترین G داریم:
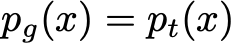
بنابراین ، ما نشان داده ایم که ، در یک مورد ایده آل با ظرفیت های نامحدود مولد و متمایز کننده ، نقطه بهینه تنظیم تخاصمی به گونه ای است که مولد چگالی ای مانند همان چگالی واقعی را تولید می کند و متمایز کننده مجبور است در یکی از دو حالت، صحیح بودن را انتخاب کند. در آخر نیز توجه کنید که G این معادله را نیز حداکثر می کند
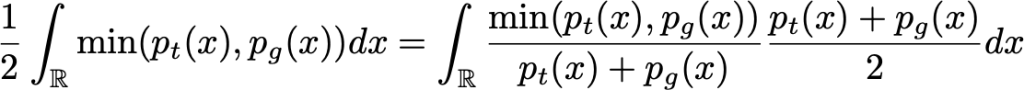
به این شکل ، ما بهتر می بینیم که G می خواهد احتمال متمایز کننده را در تشخیص اشتباه به حداکثر برساند.
برداشت ها
برداشت های اصلی از این مقاله عبارتند از:
- رایانه ها اساساً می توانند متغیر های شبه تصادفی ساده تولید کنند (به عنوان مثال می توانند متغیر هایی تولید کنند که بسیار نزدیک به توزیع یکنواخت عمل می کنند).
- روش های مختلفی برای تولید متغیر های تصادفی پیچیده تر وجود دارد از جمله مفهوم “روش تبدیل” که شامل بیان یک متغیر تصادفی به عنوان تابعی از متغیرهای تصادفی ساده تر است.
- در یادگیری ماشین ، مدل های مولد سعی می کنند داده هایی از توزیع احتمالی خاص (پیچیده) تولید کنند.
- مدل های مولد یادگیری عمیق به عنوان شبکه های عصبی (توابع بسیار پیچیده) مدل شده اند که به عنوان ورودی یک متغیر تصادفی ساده را گرفته و یک متغیر تصادفی را تولید می کنند که از توزیع احتمال هدفمند دنبال می کند (مانند “روش تبدیل”)
- این شبکه های مولد را می توان “مستقیم” آموزش داد (با مقایسه توزیع داده های تولید شده با توزیع واقعی): این ایده شبکه های مولد تطبیق دهنده است.
- این شبکه های مولد همچنین می توانند به صورت غیر مستقیم آموزش داده شوند (با تلاش برای فریب شبکه دیگری که در همان زمان آموزش داده شده است تا داده های “تولید شده” را از داده های “واقعی” متمایز کند): این ایده شبکه های مولد تخاصمی است.
شاید واژه “هیجان انگیر” که به GAN ها نسبت داده می شود کمی اغراق آمیز باشد ، ولی می توان گفت که ایده آموزش تخاصمی که توسط Ian Goodfellow و دیگر نویسندگان آن مقاله پیشنهاد شده است واقعاً عالی است. این روش برای تغییر دادن تابع ضرر از مقایسه مستقیم به غیرمستقیم واقعاً کاری است که می تواند برای دست آورد های بعدی در حوزه یادگیری عمیق بسیار الهام بخش باشد. برای نتیجه گیری ، بیایید بگوییم که ما نمی دانیم که ایده GAN ها واقعاً “جالب ترین ایده در ۱۰ سال گذشته در یادگیری ماشین” است … اما کاملاً واضح است که حداقل یکی از جالب ترین آن ها است!
ممنون از اینکه تا اینجا همراه ما بودید !
پ . ن : ما خوانندگان علاقه مند را به خواندن مقاله اولیه “شبکه عصبی تخاصمی” توصیه می کنیم ، که واقعاً مرجع خوبی برای یک مقاله علمی است ، و فیلم سخنرانی در مورد GAN های علی قدسی که واقعاً یک مدرس شگفت انگیز است ، را تماشا کنید. توضیحات اضافی را می توانید در آموزش های مربوط به GAN ها که توسط Ian Goodfellow نوشته شده اند ، در اینترنت پیدا کنید.
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب





سلام اقای مهندس یک سوال داشتم در حوزه استگانوگرافی تصاویر با شبکه های گن، در جنراتور ما یک تصویر کاور رو بهش میدیم اونجاz داره بردار تصادفی فرضا ۱۰۰تایی، بعد افزایش بعد میده میشه ۶۴×۶۴×۳ میخوام بدونم چرا z شد( G( Z. در واقع سوالم اینطوری بپرسم در شبکه مولد استگانوگرافی من میخوام بدونم: چرا باید ابعاد پیام رندم باید افزایش پیدا کنه و چرا باید ابعادش مثل تصویر باشه. ممنون میشم خیلی سریع پاسخ بدید.
سلام. فلسفه شبکه GAN همین است که از روی بردار تصادفی یک تصویر معنادار تولید (Generate) کند. لذا باید مرتبا افزایش بعد پیدا کند تا هم اندازه تصویر مورد نظر بشود. دقت کنید که استگو قرار است در تصویر اصلی مخفی شود، لذا باید هم خروجی شبکه هم اندازه تصویر اصلی باشد