درک شبکه های عصبی

در این مطلب ما چگونگی عملکرد شبکه های عصبی را به منظور ایجاد درک شهودی از یادگیری عمیق، بررسی می کنیم.

یادگیری عمیق ، موضوع داغ این روزهاست‌. اما چه چیزی آن را خاص می سازد وآن را از جنبه های دیگر یادگیری ماشین متمایز می سازد؟ این سوالی عمیق است. برای پاسخ دادن به آن ، باید اصول اولیه شبکه های عصبی را یاد بگیریم.

شبکه های عصبی، قدرت دهنده ی یاد گیری عمیق هستند و درحالی که ممکن است آن ها شبیه به جعبه سیاه باشند ، آن ها در اعماق خود سعی می کنند همان کاری که هر مدل دیگری سعی در انجام دارد را انجام دهند؛ تا پیش بینی های خوبی ارائه کنند.

دراین مقاله به بررسی شبکه های عصبی ساده می پردازیم . و تا پایان امیدوارم شما ( و من ) درکی عمیق تری از این که شبکه های عصبی چه کاری انجام می دهند، داشته باشید.

دور نما

بیایید با یک نمای کلی بالا شروع کنیم تا بفهمیم که با چه چیزی سر و کار داریم. شبکه های عصبی شبکه چند لایه از نورون ها هستند ( گره های آبی و سرخابی در نمودار زیر ) که ما برای کلاسه بندی چیزهای مختلف ، پیش بینی کردن وغیره استفاده می کنیم . نمودار زیر ّفیک شبکه عصبی ساده با پنج ورودی ، ۵ خروجی و دو لایه پنهان از نورون ها است .

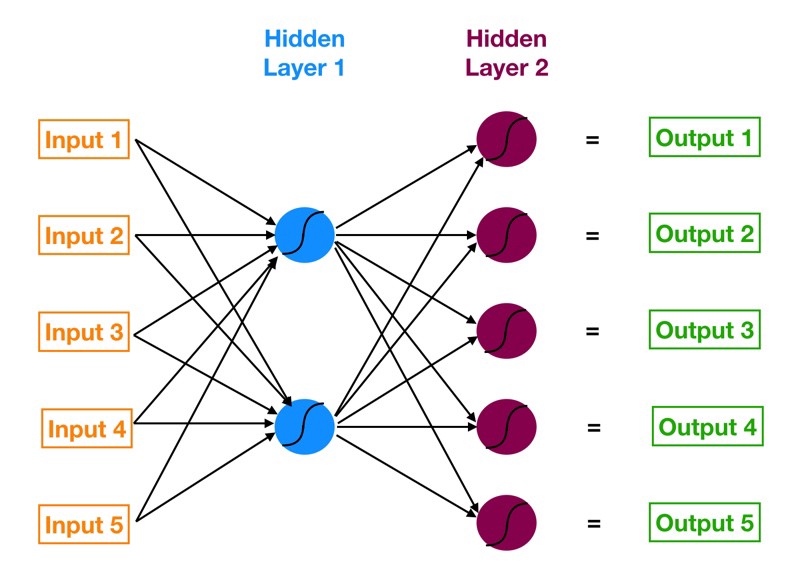
شبکه عصبی با دو لایه پنهان — شبکه های عصبی با دو لایه پنهان

از سمت چپ داریم :

لایه ورودی ما به رنگ نارنجی است.
اولین لایه پنهان از نورون ها به رنگ آبی است.
دومین لایه پنهان از نورون ها سرخابی است.
لایه خروجی ( یعنی پیش بینی مدل ما ) به رنگ سبز است .

فلش هایی که نقاط را متصل می کنند ، نشان می دهد که چگونه تمام نورون ها به هم متصل هستند و چگونه داده ها

از لایه ورودی به لایه خروجی منتقل می شوند.

بعدا هر مقدار خروجی را گام به گام محاسبه خواهیم کرد. همچنین مشاهده خواهیم کرد که چگونه شبکه عصبی از اشتباه خود با استفاده از فرآیندی به نام پس انتشار ( Backpropagation ) یاد می گیرد.

شروع به کار

اما در اولین قدم باید بدانیم که شبکه عصبی دقیقا چه کار می کند؟ آن ها مانند هر مدل دیگری، سعی در انجام پیش بینی های مناسب دارند. ما مجموعه از ورودی ها و مجموعه ای از مقادیر هدف داریم و درحال تلاش برای به دست آورد پیش بینی هایی هستیم که تا حد امکان با مقادیر هدف مطابقت دارند.

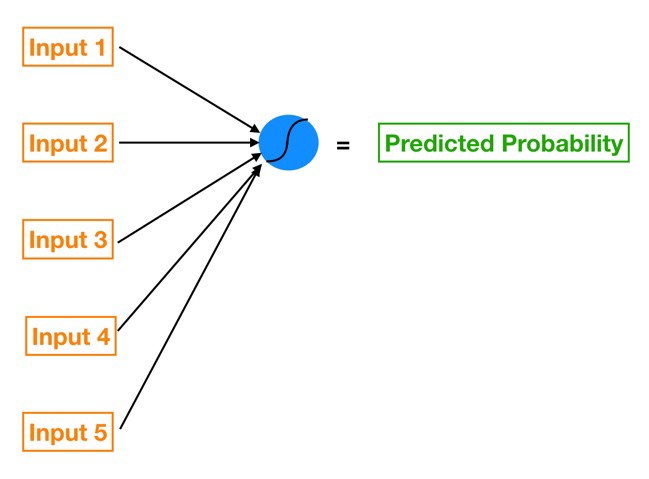
تصویر شبکه ی عصبی پیچیده ی بالا را فراموش کنید و روی این تصویر ساده تر در پایین تمرکز کنید.

شبکه عصبی رگرسیون لوجستیک — رگرسیون لجستیک ( با تنها یک ویژگی) پیاده سازی شده از طریق شبکه عصبی

این یک رگرسیون لجستیک تک ویژگی است ( ما فقط یک متغیر x را به مدل ارائه می کنیم ) که از طریق یک شبکه عصبی پردازش می شود. برای درک چگونگی اتصال آن ها می توانیم معادله رگرسیون لجستیک را با استفاده از کد های رنگی شبکه عصبی خود باز نویسی کنیم.

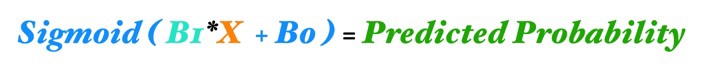
شبکه های عصبی معادله رگرسیون لوجستیک — معادله رگرسیون لوجستیک

بیایید هر عنصر را بررسی کنیم :

x (به رنگ نارنجی) ورودی ما است ، تنها ویژگی که ما به مدل خود می دهیم تا یک پیش بینی را محاسبه کنیم
B1 (به رنگ فیروزه ای یا سبز آبی) پارامتر گرادیان برآورده شده در رگرسیون لجستیک ما است؛ B1 در مورد میزان تغییر شرط نسبت به تغییرات x به ما می گوید. توجه داشته باشید کهB1 در خط فیروزه ای حضور دارد، که ورودی x را به نورون آبی در لایه پنهان متصل می کند .
B0 (به رنگ آبی) بایاس نام دارد؛ بسیار شبیه به اصطلاح وقفه در رگرسیون. تفاوت کلیدی این است که در شبکه های عصبی ، هر نروم بایاس خود را دارد ( در حالیکه در رگرسیون ، این مدل تنها یک وقفه ی دارد. )
نورون آبی نیز شامل یک تابع فعال سازی ( Activation Function ) سیگموئید است ( نشان داده شده توسط خط خمیده درون دایره آبی). به یاد داشته باشید که تابع سیگموئید همان چیزی است که ما برای رسیدن از ورودی به احتمال خروجی استفاده می کنیم.
و درنهایت احتمال پیش بینی شده را با اعمال تابع سیگموئیدی به مقدار (B1*X + B0) بدست می آوریم.

خیلی بد نبود، نه؟ پس اجازه دهید جمع بندی کنیم . یک شبکه عصبی بسیار ساده متشکل از اجزای زیر است :

یک اتصال ( گرچه در عمل ، معمولا چندین ارتباط وجود دارد ، هر یک با وزن خودش ، به نورون خاصی می رود ) با وزنی که درون آن وجود دارد ، که ورودی شما را تبدیل کرده ( با استفاده از ( B1 و آن را به نورون معرفی می کند.
نورونی که شامل یک عبارت بایاس ( ( B0 و تابع فعال سازی ( سیگموئیدی در این مورد) است.

و این دو شی بلوک های سازنده ی شبکه عصبی هستند. شبکه های عصبی پیچیده تر فقط مدل هایی هستند که لایه های پنهان تری دارند و این به آن معنی است که نرون های بیشتر و اتصالات بیشتری بین نورون ها دارند و این شبکه پیچیده تر از اتصالات ( و وزن ها و بایاس ها ) همان چیزی است که به شبکه عصبی اجازه می دهد تا روابط پیچیده پنهان در داده های ما را ” یاد ” بگیرد.

بیایید کمی پیچیدگی به آن اضافه کنیم

حالا که چارچوب اصلی خود را داریم ، اجازه دهید به شبکه عصبی کمی پیچیده تر برگردیم و ببینیم که این شبکه چگونه از ورودی به خروجی میرود. در اینجا دوباره به مرجع برمی گردیم :

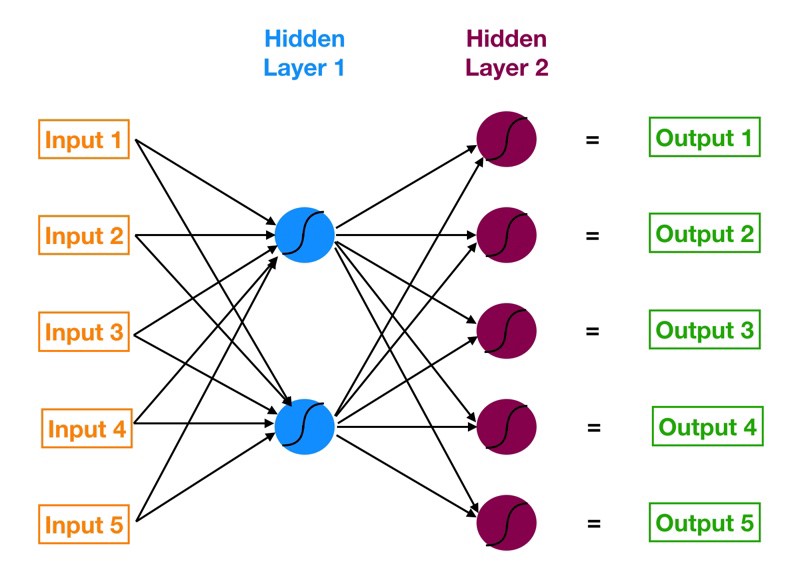
شبکه ی عصبی پیچیده تر — شبکه عصبی پیچیده تر ما

اولین لایه مخفی متشکل از دو نورون است . بنابراین برای اتصال تمام پنج ورودی به نورون های لایه پنهان ، به ده اتصال نیاز داریم. تصویر بعدی ( زیر ) فقط اتصالات بین لایه ورودی و لایه پنهان را نشان می دهد.

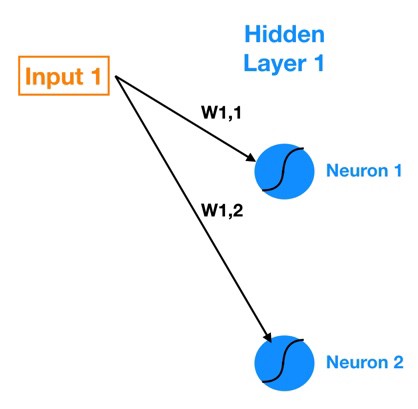
شبکه عصبی اتصال ورودی و لایه پنهان — اتصالات بین لایه ورودی و لایه مخفی

نماد گذاری ما برای وزن های موجود در اتصالات را در نظر بگیرید. W1,1 نشان دهنده ی وزن موجود در اتصال بین ورودی ۱ و نورون ۱ است و W1,2 نشان دهنده ی وزن موجود در اتصال بین ورودی ۱ و نورون ۲ است. پس نماد عمومی که من از آن پیروی می کنم ، Wa,b است که وزن اتصال بین ورودی a (نورون a) و نورون b را نشان می دهد.

حال اجازه دهید خروجی هر یک از نورون ها را در لایه پنهان ۱ ( با نام فعال سازی ) محاسبه کنیم. ما این کار را با استفاده از فرمول های زیر انجام می دهیم.

Z1 = W1*In1 + W2*In2 + W3*In3 + W4*In4 + W5*In5 + Bias_Neuron1

Neuron 1 Activation = Sigmoid(Z1)

میتوانیم از ریاضی ماتریسی برای خلاصه کردن این محاسبات استفاده کنیم ( قوانین نماد گذاری ما را به یاد داشته باشید ؛ برای مثال W4,2 وزن اتصال بین ورودی ۴ و نورون ۲ را نشان می دهد ).

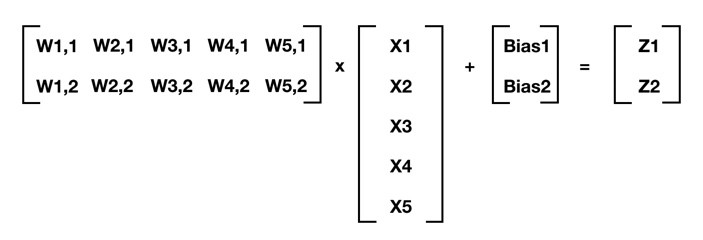
شبکه های عصبی ریاضی ماتریسی — ریاضیات ماتریسی زندگی ما را آسان تر می کند

برای هر لایه از یک شبکه عصبی که لایه قبل ازآن m عنصر عمق دارد و لایه فعلی n عنصر عمق دارد، به صورت زیر صدق می‌کند:

[W] @ [X] + [Bias] = [Z]

که [W] ماتریس n در m وزن شما (ارتباط بین لایه قبلی و لایه فعلی)، [X] ماتریس m در ۱ است که یا ورودی های اولیه است و یا فعال سازی لایه قبلی، [Bias] یک ماتریس n در ۱ از بایاس های نورون است، و [Z] یک ماتریس n در ۱ از خروجی‌های میانی است. در معادله قبلی، من از نماد های پایتون پیروی می کنم و از @ برای نشان دادن ضرب ماتریس‌ها استفاده می‌کنم. هنگامی که [Z] را بدست آوردیم، می‌توانیم تابع فعال ‌سازی (سیگموئید در این مورد ما) را به هر عنصر [Z] اعمال کنیم و که خروجی‌های نورونی ( فعال سازی ) را برای لایه فعلی به ما می‌دهد.

در نهایت، قبل از اینکه پیش برویم، اجازه دهید به صورت تصویری هر یک از این مولفه‌ ها را بر روی نمودار شبکه عصبی خود قرار دهیم تا همه آن را گرد آوری کنیم. ( [Bias] در نورون‌های آبی تعبیه شده‌ است).

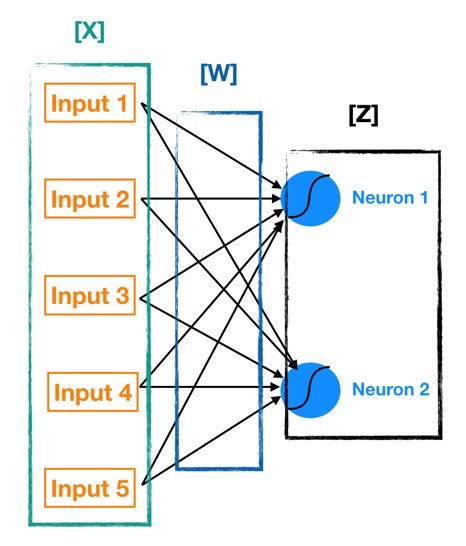
با محاسبه مکرر [Z] و اعمال تابع فعال برای هر لایه متوالی، ما می‌توانیم از ورودی به خروجی حرکت کنیم.این فرآیند به عنوان پیش انتشار ( Forward Propagation ) می‌شود. حال اکه ما می‌دانیم خروجی ‌ها چگونه محاسبه می‌شوند، زمان آن رسیده که کیفیت خروجی‌های شبکه عصبی را ارزیابی کرده و شبکه عصبی خود را آموزش دهیم.

وقت آن رسیده که شبکه عصبی آموزش ببیند

این یک پست طولانی خواهد بود پس می توانید یک وقفه ی کوتاه برای خوردن قهوه داشته باشید. هنوز با من هستید؟ بسیار عالی! اکنون که می‌دانیم چگونه مقادیر خروجی شبکه عصبی محاسبه می‌شوند, زمان آن رسیده که آن را آموزش دهیم.

فرآیند آموزش یک شبکه عصبی در سطح بالا، مانند بسیاری از مدل‌های علوم داده‌های دیگر است؛ یک تابع هزینه تعریف کنید و از بهینه سازی گرادیان نزولی برای به حداقل رساندن آن استفاده کنید.

ابتدا اجازه دهید در مورد اینکه چگونه می‌توانیم تابع هزینه را به حداقل برسانیم فکر کنیم. در رگرسیون سنتی خطی یا لجستیک، ما به دنبال ضرایب بتا (b0, b1, b2, b) هستیم که تابع هزینه را به حداقل می‌رساند. برای یک شبکه عصبی, ما همان کار را انجام می‌دهیم، اما در مقیاس بسیار بزرگ‌ تر و پیچیده ‌تر.

در رگرسیون سنتی، ما می‌توانیم هر بتا خاص را بدون تاثیر بر سایر ضرایب بتا تغییر دهیم. بنابراین با اعمال شوک ‌های ایزوله شده کوچک به هر ضریب بتا واندازه‌ گیری تاثیر آن بر تابع هزینه، به سادگی می توانیم متوجه شویم که در کدام جهت باید به سمت کاهش و در نهایت به حداقل رساندن تابع هزینه حرکت کنیم.

شبکه عصبی رگرسیون لوجستیک با 5 ویژگی — پنج رگرسیون لجستیک که با استفاده از یک شبکه عصبی انجام شد

در یک شبکه عصبی، تغییر وزن هر اتصال ( یا بایاس یک نورون ) بر روی تمام نورون‌ های دیگر و فعال سازی آن‌ها در لایه‌های بعدی تاثیر می‌گذارد.

به این دلیل است که هر نورون در یک شبکه عصبی شبیه به مدل کوچک است. به عنوان مثال، اگر یک رگرسیون لجستیک پنج ویژگی می‌خواستیم، می‌توانیم آن را از طریق یک شبکه عصبی، مانند شبکه ی عصبی سمت چپ، با استفاده از یک نورون منفرد، بیان کنیم!

بنابراین هر لایه پنهان از یک شبکه عصبی یک دسته ازمدل‌ ها ( هر نورون مجزا در لایه مانند مدل خودش عمل می‌کند ) است که خروجی‌ های آن به مدل‌های بیشتری در پایین‌ دست تغذیه می‌ شود (هر لایه پنهان ازشبکه عصبی دارای

نورون های بیشتری است).

تابع هزینه ( The Cost Function )

پس با توجه به همه این پیچیدگی ها، چه کاری می ‌توانیم بکنیم؟ در حقیقت انقدرها هم بد نیست. بیایید این کار را گام‌ به ‌گام انجام دهیم. اول، اجازه دهید به طور واضح هدف خود را بیان کنیم. با توجه به مجموعه ‌ای ازورودی‌ های آموزشی ( ویژگی‌های ما ) و پیامد ها ( هدفی که ما سعی داریم پیش‌بینی کنیم ):

ما می‌خواهیم مجموعه وزن‌ها ( به یاد داشته باشید هر خط اتصال بین هر دو عنصر در یک شبکه عصبی دارای وزن است) و بایاس ها (هر نورون یک بایاس دارد) را پیدا کنیم که تابع هزینه را به حداقل می‌رسانند ؛ که منظور از تابع هزینه، تقریبی از این است که پیش‌بینی ‌های ما چخ نسبتی با نتیجه هدف نسبی دارند.

برای آموزش شبکه عصبی ما از ورش میانگین مربعات خطا (Mean Squared Error (MSE) ) به عنوان تابع هزینه استفاده می کنیم:

MSE = Sum [ ( Prediction – Actual )² ] * (۱ / num_observations)

میانگین مربعات خطای یک مدل به ما نشان می‌دهد که ما چقدراشتباه می‌کنیم، اما با یک پیچش؛ با مربع کردن خطا های پیشبینی ها پیش از میانگین گرفتن از آن ها، ما پیش‌بینی ‌هایی را که نسبت به مقدار نهایی بسیار فاصله دارند را بیشتر از آن‌هایی که کمی دورتر هستند، اصلاح می کنیم. توابع هزینه رگرسیون خطی و رگرسیون لجستیک به روش بسیار مشابهی عمل می‌کنند.

بسیار خوب، ما یک تابع هزینه برای به حداقل رساندن آن داریم. زمان انجام گرادیان نزولی فرا رسیده است.

دست نگه دارید؛ برای استفاده از گرادیان نزولی، ما نیاز داریم که گرادیان تابع هزینه خود را که بردار ایست که به سمت بیشترین استحکام اشاره می‌کند (ما می‌خواهیم به طور مکرر در جهت مخالف گرادیان حرکت کنیم تا در نهایت به حداقل برسیم).

با این تفاوت که در یک شبکه عصبی ما بسیاری از وزن ‌های تغییر پذیر و بایاس هایی که همگی به هم متصل هستند را داریم. آیا ما گرادیان همه این ها را محاسبه خواهیم کرد؟ دربخش بعدی خواهیم دید که چگونه پس انتشار ما کمک می‌کند تا با این مشکل مقابله کنیم.

بررسی سریع گرادیان نزولی ( Gradient Descent )

گرادیان یک تابع، برداری است که عناصر آن مشتقات جزیی آن نسبت به هر پارامتر هستند. برای مثال اگر بخواهیم تابع هزینه C(B0, B1) را تنها با دو پارامترمتغیر B0 و B1 کمینه کنیم, گرادیان به صورت زیر خواهد بود:

Gradient of C(B0, B1) = [ [dC/dB0], [dC/dB1] ]

بنابراین هر مولفه گرادیان به ما می‌گوید که اگر یک تغییر کوچک را به آن پارامترخاص اعمال کنیم، چگونه تابع هزینه تغییر می‌کند؛ بنابراین ما می‌دانیم که چگونه و به چه میزان تغییر دهیم. برای جمع‌ بندی می‌توان این مراحل را به حداقل رساند :

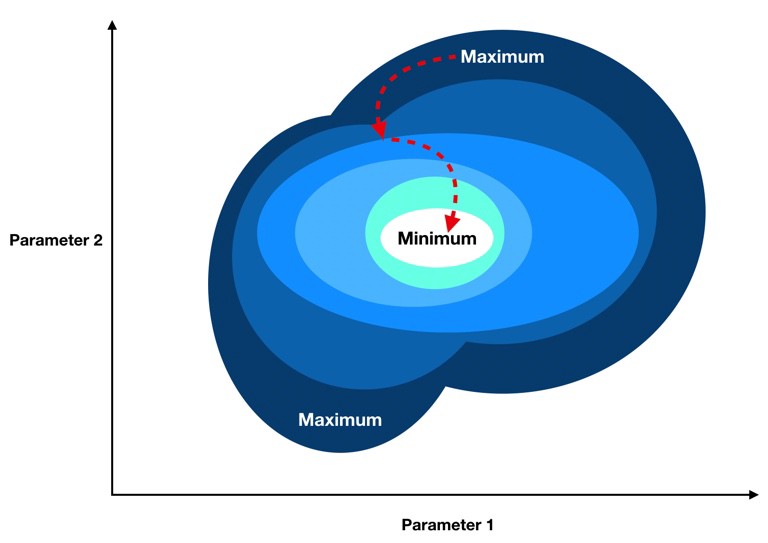
نمایش گرادیان نزولی — نمایی از گرادیان نزولی

گرادیان موقعیت فعلی ما را محاسبه کنید (گرادیان استفاده از مقادیر پارامتر فعلی ما را محاسبه کنید).
هرپارامتر را با مقدار متناسب با المان گرادیان آن و درجهت مخالف عنصر گرادیان آن اصلاح کنید. برای مثال،اگر مشتق جزیی تابع هزینه ما با نسبت به B۰ مثبت باشد اما مشتق نسبی نسبت به B۱ منفی و بزرگ باشد آنگاه ما باید B۰ را با مقدار کمی کاهش داده و B۱ را به مقدار زیادی افزایش دهیم تا تابع هزینه کاهش یابد.
گرادیان را با استفاده از مقادیر پارامتر تغییر یافته یجدید مجددا محاسبه می کنیم و گام‌های قبلی را تا زمانی که به حداقل برسیم، تکرار کنیم.

پس انتشار ( Backpropagation )

من شما را برای ریاضی مفصل این مبحث شما را به این سایت ارجاع می دهم (اگر می‌خواهید شبکه‌ های عصبی را عمیق ‌تر درک کنید، حتما آن را بررسی کنید). در عوض، ما نهایت تلاش خود را برای ایجاد درک شهودی از چگونگی و چرایی استفاده از پس انتشار انجام خواهیم داد.

به یاد داشته باشید که پیش انتشار فرآیند حرکت رو به جلو از طریق شبکه عصبی ( از ورودی به خروجی نهایی یا پیش ‌بینی ) است. پس انتشار معکوس آن است. تفاوت این است که به جای سیگنال، ما خطا را در مدل خود به عقب انتشار می دهیم.

برخی از تصورات ساده زمانی که تلاش می‌کردم روند پس انتشار را درک کنم، به من خیلی کمک کرد. در زیر تصویر ذهنی من از یک شبکه عصبی ساده وجود دارد که جلو می‌رود و از ورودی به خروجی گسترش می‌یابد. این فرآیند را می‌توان با مراحل زیرخلاصه کرد:

ورودی‌ها به لایه آبی نورون‌ها تغذیه می‌شوند و توسط وزن‌ها، بایاس، و سیگموئید در هر نورون برای بدست آوردن فعال سازی بهینه می شوند. برای مثال :

Activation_1 = Sigmoid( Bias_1 + W1*Input_1 )

فعال‌سازی ۱ وفعال‌سازی ۲، که خروجی لایه آبی هستند، به نورون سرخ آبی داده می‌شوند، که از آن‌ ها برای تولید آخرین فعال‌سازی خروجی استفاده می‌کند.

و هدف پیش انتشار، محاسبه فعال سازی در هر نورون برای هر لایه پنهان متوالی است تا زمانی که به خروجی برسیم.

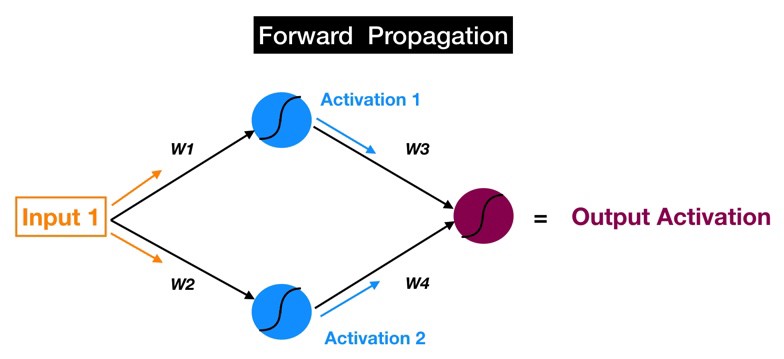
حالا اجازه دهید آن را معکوس کنیم. اگر فلش‌های قرمز (در تصویر زیر) را دنبال کنید، متوجه خواهید شد که ما اکنون از خروجی نورون سرخ آبی شروع می‌کنیم. آن نرون فعال‌ سازی خروجی ما است، که ما برای پیش‌بینی خود و مرجع نهایی خطا در مدل خود استفاده می‌کنیم. سپس این خطا را از طریق مدل خود با استفاده از همان وزن‌ ها و ارتباطاتی که ما برای پیش انتشار سیگنال خود استفاده کردیم (به جای فعال‌سازی ۱، اکنون خطا ۱ داریم؛ خطای قابل استناد به نورون بالا آبی )، جابجا می‌کنیم.

به یاد دارید که ما گفتیم که هدف پیش انتشار، محاسبه فعال سازی نورون به صورت لایه به لایه است تا زمانی که به خروجی برسیم؟ حال ما می‌توانیم هدف پس انتشار را به شیوه‌ ای مشابه بیان کنیم:

ما می‌خواهیم خطای قابل ارائه به هر نورون را (من از این به بعد این مقدار خطا را تنها به عنوان خطای نورون عنوان می‌کنم چون گفتن “قابل ارائه ” دوباره و دوباره جالب نیست) از لایه ای که به خروجی نزدیک تر است را به صورت لایه به لایه تا زمانی که به اولین لایه مدل برسیم محاسبه کنیم.

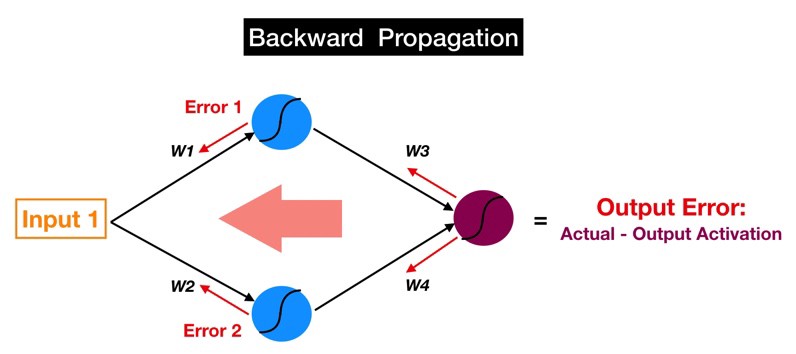
پس انتشار در شبکه عصبی — پس انتشار در یک شبکه عصبی

بنابراین چرا ما به خطا برای هر نورون اهمیت می‌دهیم؟ به یاد داشته باشید که دو بلوک سازنده یک شبکه عصبی، ارتباطاتی هستند که سیگنال‌ها را به یک نورون خاص (با یک وزن در هر اتصال) و خود نورون (با یک بایاس) منتقل می‌کنند. این وزن ‌ها و بایاس ها در کل شبکه، مقادیری هستند که ما برای تغییر پیش ‌بینی ‌های انجام ‌شده توسط مدل، تغییر دهیم.

این بخش واقعاً مهم است:

بزرگی خطای یک نورون خاص (نسبت به خطا های سایر نورون‌ ها) به‌ طور مستقیم متناسب با تاثیر خروجی نورون ( فعال‌ سازی ) بر روی تابع هزینه است.

بنابراین خطای هر یک از نورون ‌ها یک جایگزین برای مشتق جزئی تابع هزینه نسبت به ورودی‌های آن نورون است. این امر یک درک شهودی به ما می دهد؛ در صورتی که یک نورون خاص خطای بسیار بیشتری نسبت به سایرنورون ‌ها داشته باشد, پس تغییر وزن‌ ها و بایاس این نورون نسبت به هر یک از نورون‌های دیگر, تاثیر بیشتری بر خطای کل مدل ما خواهد داشت.

و مشتقات جزیی با توجه به هر وزن و بایاس, عناصری هستند که بردار گرادیان تابع هزینه را تشکیل می‌دهند. بنابراین پس‌انتشا خطا به ما این امکان را می‌دهد تا خطای قابل انتساب به هر نورون را محاسبه کنیم و در نهایت به ما اجازه محاسبه گرادیان را می دهد تا بتوانیم از گرادیان نزولی استفاده کنیم. هورا!

یک تشبیه که به ما کمک می‌کند : “بازی تقصیر”

هضم این موضوع شاید دشوار باشد، بنابراین این تشبیه به شما کمک خواهد کرد. تقریباً هر کسی یک همکار بد در

زندگی خود داشته ‌است؛ کسی که همیشه بازی تقصیر را انجام می‌دهد و همکاران و زیردستان را در زمانی که اوضاع خراب شده باشد، مقصر جلوه می دهد.

نورون‌ها، از طریق پس انتشار، استادان بازی مقصر هستند. هنگامی که خطا به نورون خاصی پس انتشار داده می شود، آن نورون به سرعت و به طور موثر انگشتش را به همکار بالادست خود (یا همکارانش) نشانه می رود که بیشتر دراثر ایجاد خطا مقصر هستند (به عنوان مثال: نورون‌ های لایه ۴ انگشت را به سمت نورون ‌های لایه ۳ و نورون های لایه ۳ به سمت نورون های لایه ۲ و به همین صورت نشانه می روند).

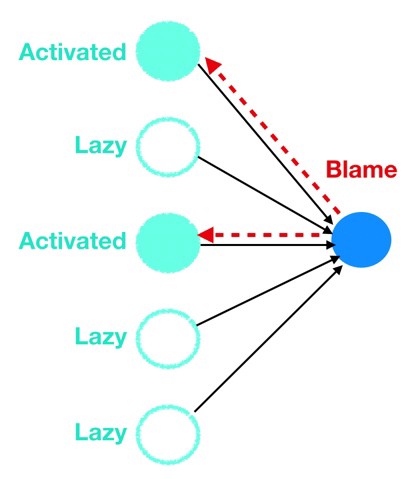
شبکه عصبی بازی تقصیر نورون ها — نورون‌ها اغلب نورون‌ها رو به بالا را مورد سرزنش قرار می‌دهند

و چگونه هر نورون می‌داند که چه کسی مقصر است، با توجه به این که نورون‌ها نمی‌توانند مستقیماً خطا های دیگر نورون‌ ها را مشاهده کنند؟ آن‌ها فقط به این نگاه می‌کنند که چه کسی برای آن‌ها بیش‌ ترین سیگنال را از نظر بالاترین و پر تکرار ترین فعال سازی فرستاده‌ است. درست مانند زندگی واقعی، افراد تنبل که جانب ایمنی را رعایت می کنند (فعال سازی های کم و کم تکرار) کمتر سرزنش می شوند در حالی که نورون‌ هایی که بیش ترین کار را انجام می‌دهند، وزن و بایاس خود را تغییر می‌دهند. بله، اما برای رساندن ما به مجموعه بهینه وزن‌ها و بایاس ها که تابع هزینه ما را به حداقل می ‌رسانند، نیز بسیار موثر است. سمت چپ تصویری است از مقصر کردن نورون‌ها توسط یک دیگر.

و این به طور خلاصه، نظریه ی فرآیند پس انتشار است. به عقیده ی من، سه هدف اصلی برای پس انتشار وجود دارد:

پس انتشار فرآیند تغییر دادن خطای لایه به لایه به سمت عقب و نسبت دادن مقدار صحیح خطا به هر نورون در شبکه ی عصلی است.
خطای قابل ارائه به هر نورون خاص مقیاس مناسبی برای تعیین این که چگونه تغییر وزن آن نورون ( ازاتصالات منتهی به نورون ) و بایاس بر تابع هزینه تاثیر می گذارد.
وقتی به عقب نگاه می کنید، بیشتر نورون‌های فعال ( بجز نرون های تنبل ) آن‌هایی هستند که مورد سرزنش قرار می‌گیرند و از طریق فرآیند پس انتشار تغییر می یابند.

جمع‌بندی کنیم

اگر همه این مطالب را تا اینجا خوانده باشید، پس شما قدردانی و تحسین مرا (برای مداومت خود) دارید.

ما با یک سوال شروع کردیم، “چه چیزی باعث خاص بودن یادگیری عمیق می‌شود؟ ” اکنون سعی می کنم که به این سوال پاسخ دهم (عمدتا از دیدگاه شبکه‌های عصبی پایه و نه انواع پیشرفته ی آن مانند CNN ها ، RNN ها و غیره).

به نظر من، جنبه ‌های زیر شبکه ‌های عصبی را خاص می ‌کنند:

هر نورون برای خودش یک مدل کوچک با بایاس خود و مجموعه ویژگی‌های ورودی و وزن ها است
هر مدل یا نورون منحصر به فرد در تمام لایه‌های پنهان این مدل به نورون‌های متعدد دیگری تغذیه می‌کند. بنابراین ما به مدل‌های متصل به مدل‌ های دیگر به روشی که مجموع آن‌ ها بزرگ ‌تر از اجزای آن است، می رسیم. این به شبکه‌های عصبی اجازه می‌ دهد تا تمام گوشه‌ ها وشکاف‌ های داده‌ های ما، شامل بخش‌های غیر خطی (اما مراقب سر ریز آن باشید؛ و مخصوصا تنظیم کردن ( Regularization ) را برای حفاظت از مدل شما در برابر کاهش کارایی هنگام مواجهه با

داده‌های جدید و خارج از نمونه) را در نظر بگیرید.

تطبیق پذیری بسیاری از مدل‌های متصل به هم و توانایی فرآیند پس انتشار برای تنظیم کارآمد و بهینه ی وزن‌ها و بایاس ها

هر مدل به شبکه عصبی اجازه می‌ دهد تا از داده به روش‌هایی که بسیاری از الگوریتم‌های دیگر نمی‌توانند، ” یاد بگیرد “.