در این پست قصد داریم در مورد توصیف گر هیستوگرام شیب های جهت دار ( HOG ) بحث کنیم. هر چند این توصیف کننده در Matlab، OpenCV و برخی کتابخانه های دیگر پیاده سازی شده اما آشنایی با جزئیات پیاده سازی این توصیف گر کمک می کند تا بتوانیم به بهترین نحو از آن استفاده کنیم.
مقاله مرتبط : هیستوگرام شیب های جهت دار (بخش اول)
گام سوم- محاسبه ی هیستوگرام گرادیان در سلول های ۸*۸
در این مرحله تصویر به سلول های ۸*۸ تقسیم شده و هیستوگرام گرادیان برای هر کدام از این سلول ها محاسبه خواهد شد. اما چرا تصویر را به سلول های ۸*۸ تقسیم کردیم؟
یکی از مهم ترین دلایل استفاده از توصیف گرها این است که تصاویری که اغلب حجم بالایی دارند را تبدیل به بردارها یا آرایه هایی کوچک و جمع و جور می کند. یک تکه ی ۸*۸ از تصویر ۱۹۲=۳*۸*۸ مقدار شدت روشنایی دارد. گرادیان این تکه ی تصویر نیز به ازای هر پیکسل دو مقدارِ اندازه و شیب دارد که در مجموع ۱۲۸=۲*۸*۸ عدد می شود. در انتهای این بخش خواهیم دید که چطور این ۱۲۸ عدد بوسیله ی یک هیستوگرام ۹ قسمتی نمایش داده خواهد شد. این نحوه ی نمایش تصویر را کم حجم خواهد کرد. نه تنها این روشِ توصیف، فشرده تر است بلکه نسبت به نویز مقاوم تر نیز هست. شیب هر پیکسل به تنهایی ممکن است نویز داشته باشد اما هیستوگرام یک تکه تصویر ۸*۸ کمتر به نویز حساس است.
اما چرا تکه های ۸*۸ تایی و چرا مثلا تکه های ۳۲*۳۲ تایی نه؟ این عدد در حقیقت با سعی و خطا بدست آمده است. هیستوگرام شیب های جهت دار ( HOG ) در ابتدا برای تشخیص عابر پیاده استفاده شد. سلول های ۸*۸ پیکسلی در تصویری از یک عابر پیاده که به مقیاس ۱۲۸*۶۴ پیکسلی تغییر اندازه یافته، آن قدر بزرگ هست که ویژگی های مورد نظرمان را استخراج کند. و اما هیستوگرام…! هیستوگرام در واقع یک بردار ۹ تایی (۹ قسمتی) است که هر قسمت ( bin ) آن متناظر با زوایای ۲۰، ۴۰، ۶۰، …. ۱۶۰ است.
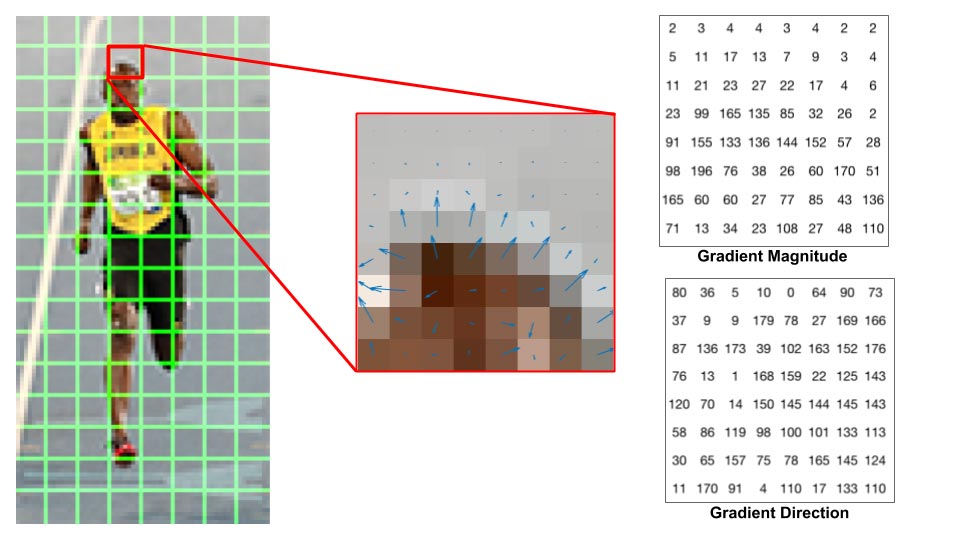
تصویر راست: همان شیب ها در قالب اعداد نشان داده شده اند.
اگر در بینایی ماشین تازه کار هستید تصاویر بالا بسیار آموزنده اند. در تصویر وسط جهت پیکان ها نشان دهنده ی جهت شیب و اندازه پیکان نمایش گر بزرگی شیب است. توجه کنید که جهت پیکان ها همراستا با تغییرات شدت روشنایی است و اندازه پیکان ها نشان دهنده ی میزان تغییرات شدت روشنایی است.
در تصویر سمت راست اعدادی را مشاهده می کنیم که اندازه و زاویه گرادیان هستند؛ البته با یک اختلاف کوچک و آن این که زوایا بجای آن که بین ۰ تا ۳۶۰ درجه باشند بین ۰ تا ۱۸۰ درجه اند. این زوایا را زاویه های بدون علامت می گویند زیرا در آن ها زاویه و قرینه ی آن زاویه با یک عدد نشان داده می شود. به تجربه ثابت شده که برای تشخیص عابر پیاده زوایای بدون علامت نسبت به زوایای علامت دار نتایج بهتری دارند.
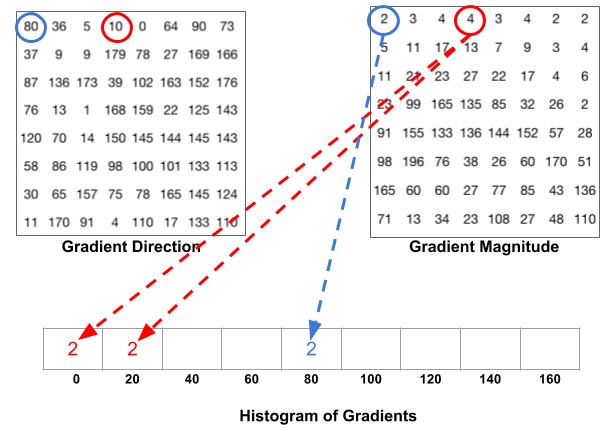
قدم بعدی تولید هیستوگرام در هر کدام از سلول های ۸*۸ پیکسلی است. روند تولید هیستوگرام بدین نحو است که بر اساس زاویه ی شیب پیکسل، bin هیستوگرام انتخاب شده و طبق اندازه ی شیب آن پیکسل به bin منتخب رای داده می شود. بهتر است مثالی را بررسی کنیم. در تصویر پایین زاویه پیکسلی که با رنگ آبی مشخص شده ۸۰ درجه و اندازه آن ۲ می باشد. بنابراین طبق آنچه گفته شد عدد ۲ را به پنجمین bin هیستوگرام اضافه می کنیم. اما زاویه پیکسلی که به رنگ قرمز در آمده ۱۰ درجه و اندازه اش ۴ است. از آنجا که زاویه ۱۰ درجه درست وسط زوایای ۰ و ۲۰ درجه است، بنابراین مقدار ۴ بطور مساوی بین قسمت های ۰ و ۲۰ درجه قسمت می شود.
از آنجا که می دانیم زوایای حول وحوش ۰ و ۱۸۰ درجه هم ارزند بنابراین اگر زاویه شیبی بزرگ تر از ۱۶۰ درجه بود آن زاویه در حقیقت بین ۱۶۰ و ۱۸۰ درجه است. در مثال زیر اندازه ی پیکسلی که زاویه ۱۶۵ درجه دارد بطور متناسب بین bin های ۰ و ۱۶۰ درجه تقسیم می شود.
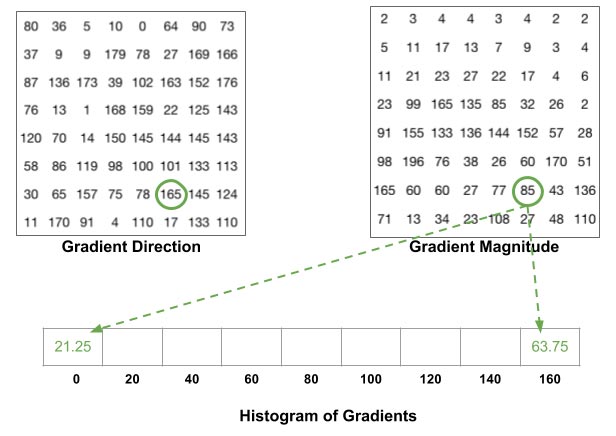
هیستوگرام سلول ۸*۸ بالا نزدیک به تصویر پایین خواهد بود :
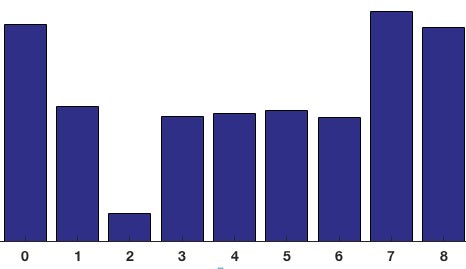
همان طور که گفته شد، محور Y صفر درجه است. در هیستوگرام بالا به وضوح مشهود است که زوایای نزدیک به ۰ و ۱۸۰ درجه آرای بالایی داشته اند. این بدین معناست که جهت پیکسل ها در سلول تحت بررسی بیشتر به سمت بالا یا پایین بوده اند.
گام چهارم – نرمالیزاسیون بلوک های ۱۶*۱۶
 در مرحله ی قبل، هیستوگرام بر اساس گرادیان تصویر بدست آمد. گرادیان های یک تصویر به روشنایی حساس اند. مثلا اگر با تقسیم تمام پیکسل ها بر ۲ تصویر را تاریک تر کنیم، اندازه ی گرادیان نصف خواهد شد و بنابراین مقادیر هیستوگرام نیز نصف می شوند. شرایط مطلوب این است که توصیف کننده از شرایط نوری مستقل باشد. یکی از بهترین روش ها برای برآوردن چنین خواسته ای ”نرمالیزاسیون“ است. قبل از این که ببینیم چطور هیستوگرام نرمالایز می شود، بیایید نرمالایز کردن برداری با طول ۳ را بررسی کنیم.
در مرحله ی قبل، هیستوگرام بر اساس گرادیان تصویر بدست آمد. گرادیان های یک تصویر به روشنایی حساس اند. مثلا اگر با تقسیم تمام پیکسل ها بر ۲ تصویر را تاریک تر کنیم، اندازه ی گرادیان نصف خواهد شد و بنابراین مقادیر هیستوگرام نیز نصف می شوند. شرایط مطلوب این است که توصیف کننده از شرایط نوری مستقل باشد. یکی از بهترین روش ها برای برآوردن چنین خواسته ای ”نرمالیزاسیون“ است. قبل از این که ببینیم چطور هیستوگرام نرمالایز می شود، بیایید نرمالایز کردن برداری با طول ۳ را بررسی کنیم.
فرض کنید یک بردار رنگی RGB با مقادیر [۱۲۸, ۶۴, ۳۲] داریم. طول این بردار برابر است با √(۱۲۸^۲+۶۴^۲+۳۲^۲ )=۱۴۶/۶۴
این مقدار را نرم L2 نیز می گویند. تقسیم هر کدام از عناصر این بردار بر طول بردار بدست آمده بردار نرمالایز شده را بدست می دهد:
[۰٫۸۷,۰٫۴۳,۰٫۲۲]حال بیایید بردار دیگری را بررسی کنیم که در آن مقادیر هر کدام از عناصر این بردار، دو برابر بردار اولی است:
۲ x [128,64,32] = [256,128,64]
نرمالایز شده ی این بردار هم همان مقدار قبلی خواهد بود. اگر شک دارید امتحان کنید!! این مثال نشان می دهد که نرمالیزاسیون مقیاس را حذف می کند.
حالا که نرمال کردن بردار را دیدیم، شاید با خود بگویید، چون هیستوگرام سلول نیز در حقیقت یک بردار ۹×۱ است بنابراین برای نرمال کردن هیستوگرام نیز به همان شیوه عمل می کنیم. فکر بدی نیست! اما ایده ی بهتر آن است که نرمالیزاسیون را در ابعادی بزرگتر انجام دهیم. مثلا در بلوک های ۱۶×۱۶٫ یک بلوک ۱۶×۱۶ متشکل از ۴ هیستوگرام است که با الحاق کردن آن ها به هم یک بردار ۳۶ x 1 ساخته می شود و حالا به همان روشی که گفته شد می توان بردار نرمال را بدست آورد. همان طور که در شکل دیده می شود پنجره ۸ پیکسل جابجا شده و بردار ۳۶×۱ نرمال شده و این روند تکرار می شود.
گام پنجم – محاسبه بردار ویژگی HOG
برای محاسبه ی بردار ویژگی نهایی کل تکه تصویر مورد نظر، بردار های نرمال شده ی ۳۶×۱ برای ساخت یک بردار بزرگ به هم الحاق خواهند شد. اما اندازه ی این بردار چقدر خواهد شد؟ بیایید محاسبه کنیم!
۱ – در تصویری با اندازه ۱۲۸*۶۴ یک پنجره ۱۶*۱۶ تعداد ۷ جایگاه افقی و ۱۵ موقعیت عمودی را می تواند به خود اختصاص دهد، بنابراین این پنجره می تواند جایگاه متفاوت در تصویر داشته باشد.
۲- هر بلوک ۱۶*۱۶ توسط یک بردار ۱*۳۶ توصیف می شود. بنابراین اگر تمام این بردارها را بهم متصل کنیم برداری با طول ساخته می شود.
منبع LearnOpenCV مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب




