ضرورت ناحیه بندی خودکار
در بسیاری تصاویر در دنیای واقعی، به ویژه تصاویر با تباینِ ( Contrast ) پایین، ناحیه بندی یا استخراج دستیِ هدف، کاری بس سخت و زمان بر بوده و نیازمند دقت و مهارت است. از این میان، ذات تصاویر پزشکی به نوعی است که تباین ضعیفی دارد و بیماری هایی همچون دیابت نیز در تصویر شبکیه چشم تأثیر می گذارند و این مسائل همه و همه لزوم الگوریتم های خودکار برای ناحیه بندیِ خودکار را نشان می دهد. هدف ما از این مقاله بازگویی الگوریتم های مختلفی است که بتواند علی الرغم وجود نویز و شدت روشنایی غیریکنواخت، به خوبی تصاویر را ناحیه بندی کند. انواع روش های ناحیه بندی را می توان به چند دسته ی ریخت شناسی، چند مقیاسی، ردیابی، مبتنی بر مدل و مبتنی بر منطقه تقسیم کرد. از روش های مشهور مبتنی بر منطقه می توان به رشد ناحیه (Region Growing )، مجموعه هم تراز ( Level Set Method ) ، مار ها ( Snakes ) و مرز فعال ( Active Contour ) اشاره کرد. در ادامه، انواع روش های ناحیه بندی به تفصیل توضیح داده خواهد شد.
۱- روش های چند مقیاسی ( Multi-scale approach )
روش چند مقیاسی با دقت های مختلف تقسیم بندی را انجام می دهد. مزیت اصلی این روش افزایش سرعت پردازش است. ساختارهای عمده (مثلا عروق بزرگ در تصاویر شبکیه چشم)، از تصاویر با کیفیت پایین استخراج می شود در حالیکه دیگر ساختارها (مانند عروق نازک)، از تصاویر با وضوح بالا استخراج شده است. یکی دیگر از مزیت ها افزایش ستبری ( Robustness ) است. پس از بخشبندی ساختارهای قوی در وضوح پایین، ساختارهای ضعیف، مانند شاخه ها را، در همسایگی ساختارهای قوی می توان در وضوح بالاتر ناحیه بندی کرد.
۱-۱- تبدیل موجک گسسته ( Discrete Wavelet Transform )
تبدیل گسسته موجک یک تحلیل چند مقیاسی است که با عبور دادن سیگنال از مجموعها ی از فیلترها، حاصل می شود. سیگنال در هر مرحله از تجزیه به دو بخش تقسیم می شود: کلیات (تقریب) ( Approximation ) و جزییات ( Details ). بخش حاصل از عبور سیگنال از فیلتر بالا گذر شامل اطلاعات فرکانس بالا است و بخش حاصل از عبور سیگنال از فیلتر پایین گذر شامل اطاعات فرکانس پایین و مشخصات هویتی سیگنال است. در هر بار تجزیه یک باند فرکانسی از سیگنال جدا می شود و باقیمانده در سیگنال “تقریب” ذخیره می شود. پس تجزیه تصویر توسط موجک دو-بعدی گسسته در سطح اول، چهار تصویر به دست می دهد. تصویر اول که دارای اطلاعات فرکانس پایین است، کلیات تصویر است. سه تصویر دیگر جزییات تصویر در سه جهت افقی، عمودی و قطری می دهد. زیربنای کلیات اطلاعات تقریبی تصویر اصلی را حفظ می کند و زیربناهای جزئیِ جزئیات، شدت در سه جهت ذکر شده را ثبت می کند. از آنجایی که زیر مجموعه جزییات، دارای اطلاعات فرکانس بالاست، برای حذف نویز می توان از اطلاعات جزییات در سطوح اولیه تجزیه چشم پوشی کرد. شکل زیر تصویر تجزیه شده با جزییات افقی، عمودی و قطری را نشان می دهد.
۱-۲- ماتریس هسین ( Hessian Matrix )
یکی دیگر از تحلیل چند مقیاسی استفاده از خواص ماتریس هسین برای به دست آوردن بردارهای ویژه است. بردارهای ویژه به منظور بهبود تصویر و استخراج شی، نادیده گرفتن نویز و تشخیص ساختارهای خطی و دایروی به کار می روند. در واقع ایده اصلی پشت آنالیز بردارهای ویژۀ ماتریس هسین، استخراج جهت های اصلی است که ساختار مرتبه دومِ محلیِ تصویر می تواند تجزیه ( Decomposed ) کند. فرانگی و همکارانش از خواص ماتریس هسین برای ناحیه بندی رگ های شبکیه چشم استفاده می کند.
ماتریس هسین عبارت است از ماتریس مربعی که شامل مشتقات جزئی مرتبه دوم تابعی میباشد. این ماتریس در قرن نوزدهم میلادی توسط ریاضیدان آلمانی مطرح و به نام خود او، نام گذاری شد. در اینجا درایه های ماتریس هسین را از ضرب پیچشی تصویر با مشتق دوم گاوسین در سه جهت افقی، عمودی و مورب به دست می آید. بدین صورت که
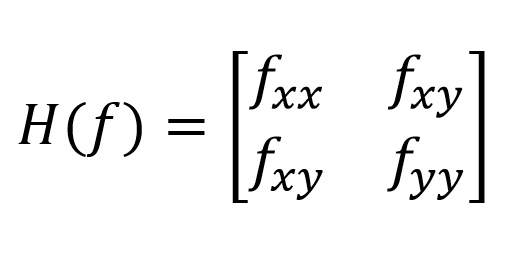
که درایه های آن برابرند با:
fxx = covolv(I,Gaussianxx)
fyy = covolv(I,Gaussianyy)
fxy = covolv(I,Gaussianxy)
که I تصویر اصلی، Gaussianxx و Gaussianyy و Gaussianxy به ترتیب مشتق دوم گاوسین در سه جهت افقی، عمودی و مورب هستند. بردارهای ویژۀ و از طریق زیر محاسبه می شوند:
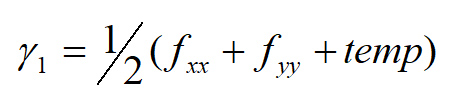
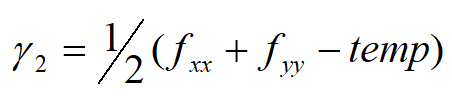
که در آن temp برابر است با:
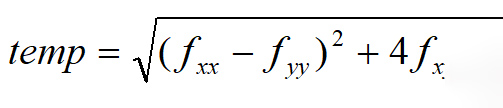
همانطور که گفته شد این بردارهای ویژه در تشخیص و تعیین رگ، پسزمینه، نویز، ساختارهای خطی، نقاط لکهمانند و غیره بسیار مهماند. ساختارهای دایروی شکل هیچ جهتِ اصلی ای ندارند. بنابراین هر دو بردار ویژه باید بهم دیگر نزدیک باشند. مقادیر ویژه بدین صورت مرتب می شود:
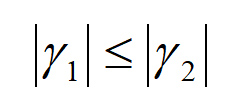
- برای جداسازی صفحه و ساختارهای خط مانند:
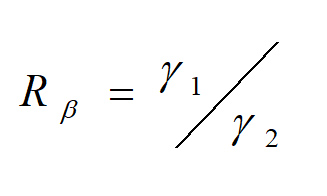
اگر Rβ→۰ یک خط را نشان می دهد و اگر Rβ→۱ نمایش دهنده دایره است .
برای تفکیک بین پیش زمینه (رگ) و پس زمینه (نویز):
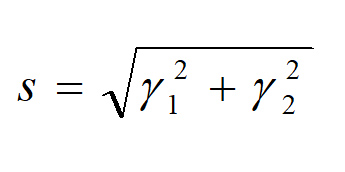
هنگامی که نزدیک به خط مرکزی رگ باشد s بالاترین مقدار را دارد. در نهایت فرمولاسیون اندازه گیری رگ بدین صورت محاسبه می شود:
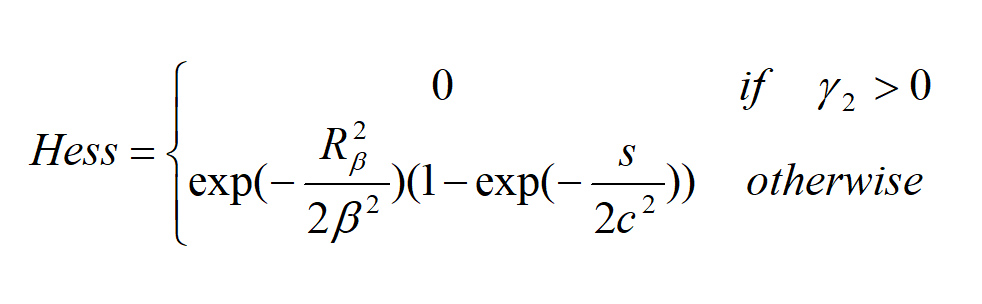
چند مقیاسی بودن یکی از ویژگی های تأثیر گذار در ناحیه بندی تصویر، به ویژه تشخیص عروق است. برای درک بهتر در شکل زیر اعمال فرمولاسیون فیلتر مبتنی بر بردارهای ویژه هسین روی تصویر شبکیه با مقیاس های مختلفِ δ در مشتق دوم گاوسین نشان داده شده است. همانگونه که در شکل دیده می شود δهای کوچکتر در استخراج عروق ظریف تر توانمند ترند. که البته حضور نویز هم در این مقیاس ها بیشتر است. به طور وارون مقیاس های بزرگتر تأکید بیشتری بر عروق ضخیم دارند و نویز را هم بیشتر می پوشانند. این دیگر مصالح های است که با توجه به نمونه باید تصمیم گرفت چه چیز مهم تر است: افزایش درصد پاسخ های صحیح یا کاهش پاسخ های غلط!
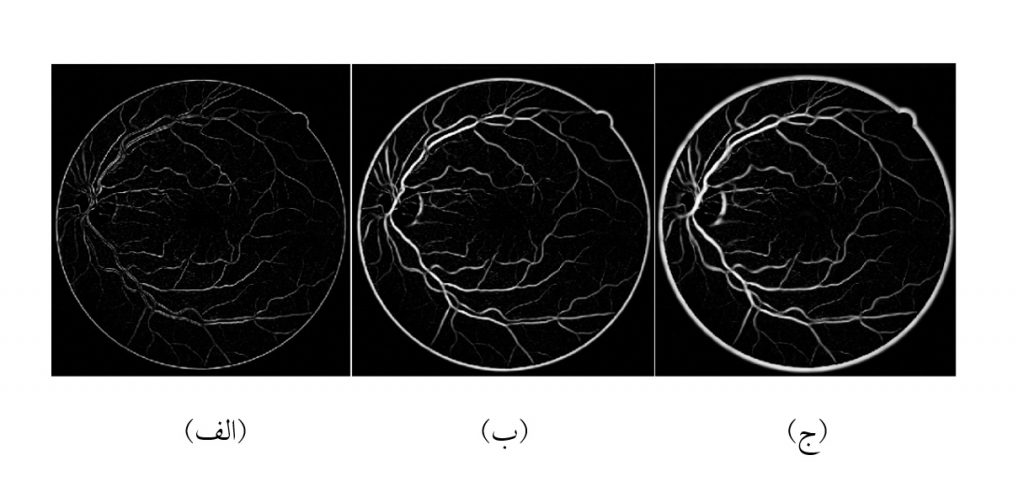
تحلیل چند مقیاسیِ روشن سازی عروق با ماتریس هسین در مقیاس های مختلفِ δ. الف) مقیاس δ=۱ ، (ب) مقیاس δ از ۱ تا ۳، (ج) مقیاس δ از ۱ تا ۵
ادامه دارد…
بیشتر بخوانید :
- ANPR یا LPR : تفاوت چیست؟
- هوش مصنوعی مولد تهدیدات جدیدی برای امنیت سایبری ایجاد می کند
- فناوری تشخیص پلاک خودرو چگونه جامعه را هوشمندتر می کند
- گوگل ساختار سازمانی خود را جهت تمرکز بر هوش مصنوعی اصلاح می کند
- پلاک خوان های شهر گرینزبوروی آمریکا فعلاً قرار نیست افزایش پیدا کنند
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب





2 نظر
دنبال کنید : آشنایی با Autoencoder ها در Tensorflow برای حذف نویز - مجله شهاب
دنبال کنید : 7 چالش بینایی رایانه ای در خودروهای خودران - مجله شهاب