رگرسیون خطی یکی از پرکاربردترین روش های مورد استفاده برای مدل سازی رابطه بین دو یا چند متغیر است. این روش می تواند در هر جایی اعمال شود، از پیش بینی فروش برای برنامه ریزی موجودی انبار گرفته تا مشخص کردن تاثیر گاز های گلخانه ای بر دمای جهانی زمین و پیش بینی کردن بازده محصول بر اساس بارش باران.
در این مقاله ما خواهیم گفت که رگرسیون خطی چیست و چگونه کار می کند، و یک مدل یادگیری ماشین برای پیش بینی میانگین امید به زندگی افراد بر اساس تعدادی از عوامل خواهیم ساخت.
رگرسیون خطی چیست؟
طبق سایت ویکی پدیا، رگرسیون خطی رویکردی خطی برای مدل سازی رابطه بین یک متغیر وابسته و یک یا چند متغیر مستقل است. به عبارت ساده تر، رگرسیون خطی «خط بهترین برازش» است که نمایانگر یک مجموعه داده است.
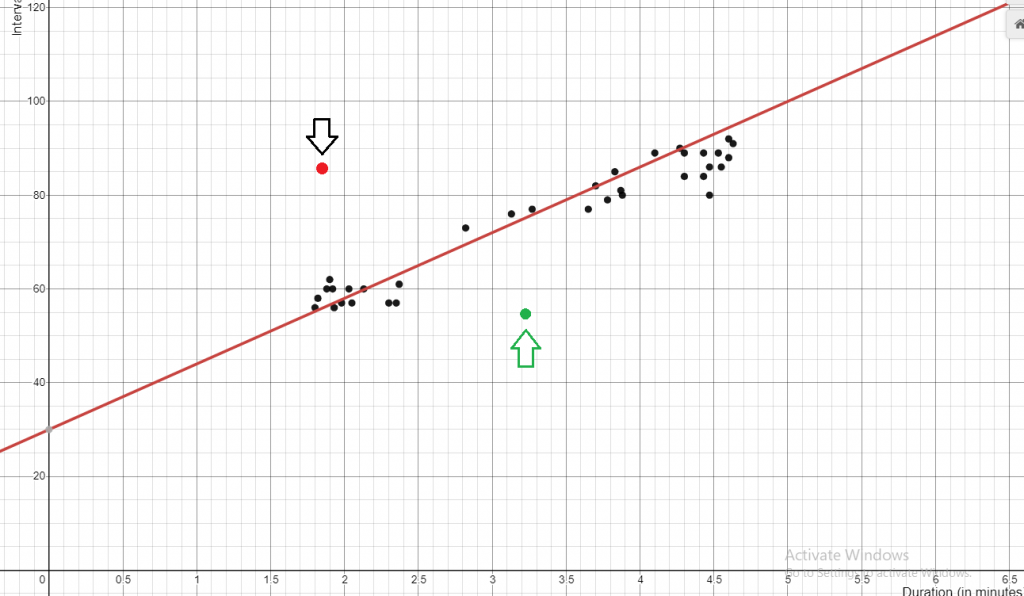
پایین مثالی از یک خط است که بهترین تناسب را با نقاط داده شده دارد. با ایجاد خطی که بهترین تناسب را دارد، می توان نقاط آینده و جای آن ها و نقاط پرت را نیز پیش بینی کرد. برای مثال، فرض کنید این نمودار نمایانگر قیمت الماس بر اساس وزن آن است. اگر نقطه قرمز را نگاه کنیم، میبینیم که این الماس دارای ارزش بیش از حد است زیرا اگر وزن این الماس را با توجه به وزن الماس های دیگر درنظر بگیریم هزینه بسیار بیشتری دارد. به طور مشابه، نقطه سبز ارزشی کمتر از حد معمول را دارد زیرا با توجه به وزن بقیه الماس ها هزینه کمتری دارد.
پس چطور باید به خط بهترین برازش دست یافت؟ بیایید راهش را بیابیم.
رگرسیون خطی ساده چگونه عمل می کند
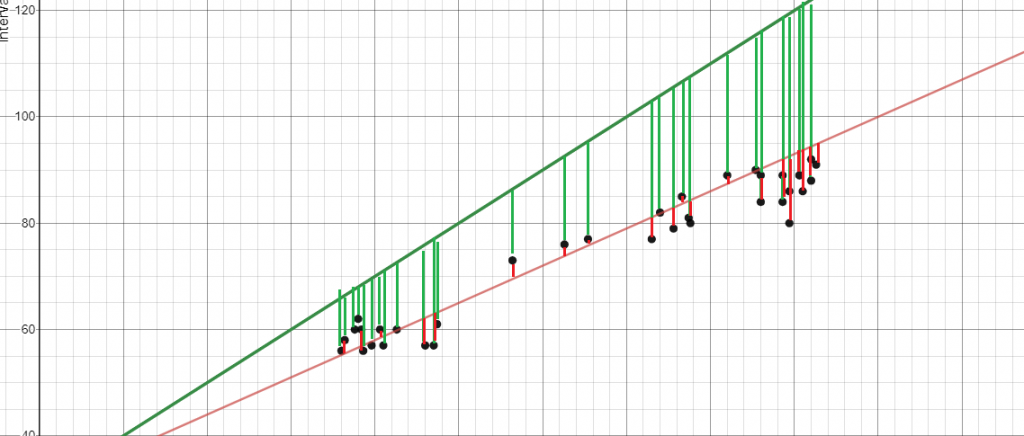
می خواهیم روی رگرسیون خطی ساده تمرکز کنیم. خط بهترین برازش یا معادله ای که داده ها را نشان می دهد، با به حداقل رساندن مجذور فاصله بین نقاط و خط بهترین برازش که همچنین مربع خطا نامیده می شود به دست می آید.
برای مثال، دو خط بهترین برازش در بالا وجود دارد، خط قرمز و خط سبز. توجه کنید که چقدر خطا (خط های سبز بین خط بهترین برازش و نمودارها) به اندازه قابل توجهی بزرگ تر از خط قرمز است. هدف رگرسیون پیدا کردن معادله ای است که در آن مجموع خطاها به حداقل رسیده باشد.
اگر مایل به پی بردن به ریاضی قضیه هستید، می توانید ویدیوهای آکادمی خان را از اینجا تماشا کنید.
اگر می خواهید از رگرسیون خطی ساده استفاده کنید می توانید از کلاس LinearRegression از کتابخانه scikit-learn استفاده کنید.
from sklearn.linear_model import LinearRegression
رگرسیون خطی چندگانه
رگرسیون خطی ساده زمانی مفید است که شما می خواهید معادله ای را بیابید که نمایانگر دو متغیر است، متغیر مستقل (x) و متغیر وابسته (y). اما وقتی متغیر های فراوانی را دارید تکلیف چیست؟ برای مثال، قیمت یک خودرو وابسته به عوامل زیادی از قبیل قدرت اسب بخار، سایز ماشین، و ارزش خود برند خودرو است.
اینجا جایی است که رگرسیون چندگانه پا به میدان می گذارد. رگرسیون چندگانه برای توضیح رابطه بین یک متغیر وابسته و بیش از یک متغیر مستقل استفاده می شود.
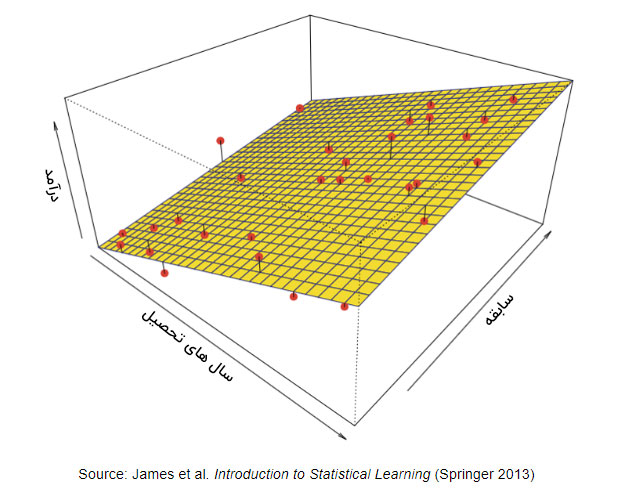
عکس زیر نموداری را بین درآمد (y) و سابقه و سال های تحصیل (x) نشان می دهد. زمانی که دو متغیر مستقل وجود دارد، به جای خط بهترین برازش یک صفحه بهترین برازش به دست می آید.
رگرسیون چند جمله ای
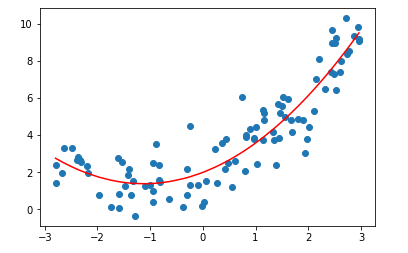
اگر شما مجموعه ای از داده ها که خط بهترین برازش آن ها خطی نباشد، داشته باشید چه (مانند عکس زیر). اینجا زمانی ست که شما از رگرسیون چند جمله ای استفاده خواهید کرد. باز هم طبق ویکی پدیا، این نوع رگرسیون به عنوان نوعی از آنالیز رگرسیون تعریف شده است که در آن رابطه بین متغیر مستقل x و متقیر وابسته y به عنوان یک چندجمله ای n امین درجه ای در x مدل سازی شده اند. به عبارتی ساده تر، این رگرسیون در یک رابطه غیرخطی بین x و y صدق می کند.
زمانی که می خواهید از رگرسیون چندجمله ای استفاده کنید، چند خط کد بیشتر مورد نیاز است.
from sklearn.preprocessing import PolynomialFeatures poly_reg = PolynomialFeatures(degree = n) #where n is equal to the number of degrees that you want
کاربرد: پیش بینی میانگین امید به زندگی
برای نشان دادن چگونگی ساخت یک مدل رگرسیون در پایتون، من از «مجموعه داده های امید به زندگی (از سازمان بهداشت جهانی) موجود در Kaggle استفاده کردم. هدفم ساختن مدلی بود که بتواند میانگین امید به زندگی یک شخص در کشوری مشخص و در سالی مشخص را با توجه به تعدادی از متغیرها پیش بینی کند. به خاطر داشته باشید که این مدلی بسیار پایه ای است.
در مورد آماده سازی داده ها، کم و بیش از مراحلی که در این پست گفته شده، استفاده شده است.
قسمت یک اینجا
قسمت دو اینجا
چند موضوع جدید وجود را من در این مدل معرفی کردم، مانند تبدیل داده های مطلق (کشور ها) به متغیرهای ساختگی و ارزیابی عامل تورم واریانس (VIF) همه متغیرها.
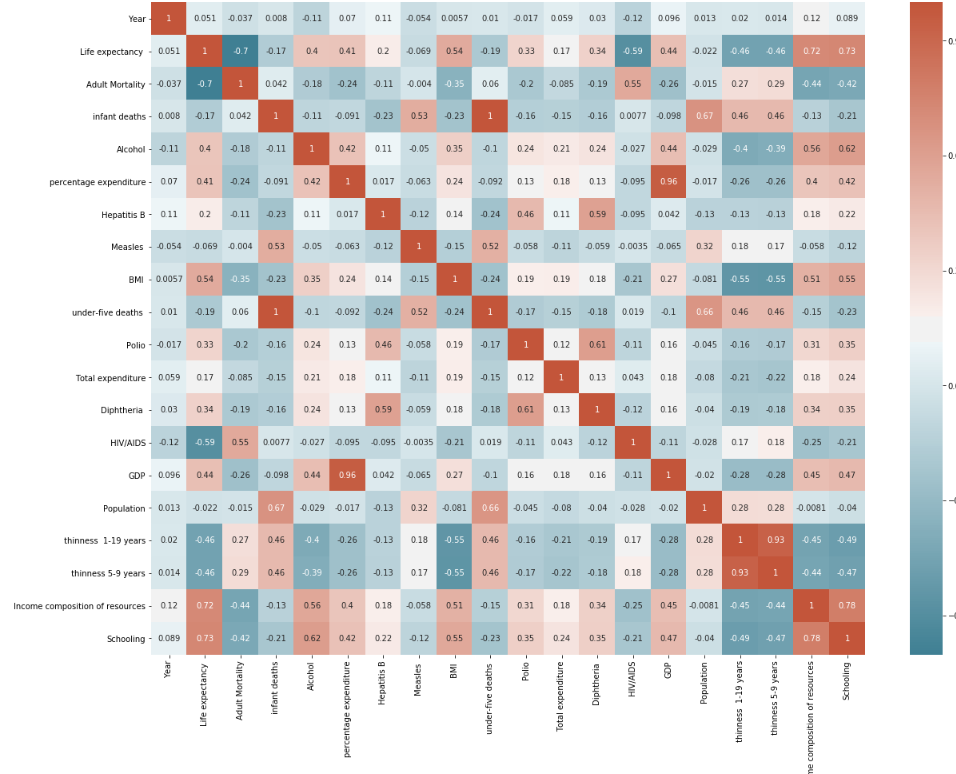
چیزی که خواستم به اشتراک بگذارم این نمایه از همبستگی ها بود چون در اینجا چند همبستگی بسیار جالب وجود دارد:
- یک همبستگی مثبت قوی ۰٫۷۳ بین «تحصیل» و «امید به زندگی» وجود دارد. این ممکن است به این دلیل باشد که آموزش بیشتر در کشورهای ثروتمند شایع است. یعنی در کشورهایی با زیرساخت، مراقبت های بهداشتی، رفاه، فساد کمتر و غیره.
- به صورت مشابه با نکته بالا، همبستگی مثبت متوسط ۰٫۴۴ بین «GPD» (تولید ناخالص داخلی) و «امید به زندگی» وجود دارد، تقریبا به همان دلیلی که گفته شد.
- در کمال تعجب، یک همبستگی مثبت متوسط ۰٫۴۰ بین «الکل» و «امید به زندگی» وجود دارد. حدس من این است که این به این دلیل است که فقط در کشورهای ثروتمند توانایی خرید و مصرف الکل وجود دارد. یا به این دلیل است که مصرف الکل در جمعیت ثروتمند متداول تر است.
# Create Model from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures poly_reg = PolynomialFeatures(degree = 2) X_poly = poly_reg.fit_transform(X) poly_reg.fit(X_poly, y) X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=.30, random_state=0) regressor = LinearRegression() regressor.fit(X_train, y_train) y_pred = regressor.predict(X_test)
بعد از پالایش داده ها، من کد بالا را اجرا کردم تا مدل رگرسیون چندگانه چند جمله ای خودم را با میانگین مطلق خطا ۸٫۲۲ و محدوده ۴۴٫۴ ایجاد کنم. امیدواریم این مطلب برای شما مفید بوده باشد.
بیشتر بخوانید :
- هوش مصنوعی مولد تهدیدات جدیدی برای امنیت سایبری ایجاد می کند
- فناوری تشخیص پلاک خودرو چگونه جامعه را هوشمندتر می کند
- گوگل ساختار سازمانی خود را جهت تمرکز بر هوش مصنوعی اصلاح می کند
- پلاک خوان های شهر گرینزبوروی آمریکا فعلاً قرار نیست افزایش پیدا کنند
- فرماندار اوکلند از پلاک خوان ها حمایت می کند اما مخالفان در اثربخشی آن تردید دارند
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب