مقدمه
ساخت یک شبکه عصبی کار ملالت آوری می باشد و این امر به منظور دستیابی به نتایج بهتر بیش از پیش چالش برانگیز خواهد بود. اولین چالش به هنگام ساخت یک شبکه عصبی، مقداردهی اولیه وزن هاست، اگر وزن ها به درستی مقداردهی اولیه شده باشد، بهینه سازی در کمترین زمان ممکن انجام خواهد شد. درغیر این صورت، همگرایی به سوی مقدار مینیمم خطا غیرممکن خواهد بود.
مقاله مرتبط :
اجازه دهید مروری از کلیت فرآیند شبکه عصبی واینکه چرا مقداردهی اولیه وزن ها برروی مدل تأثیر گذار است، داشته باشیم.
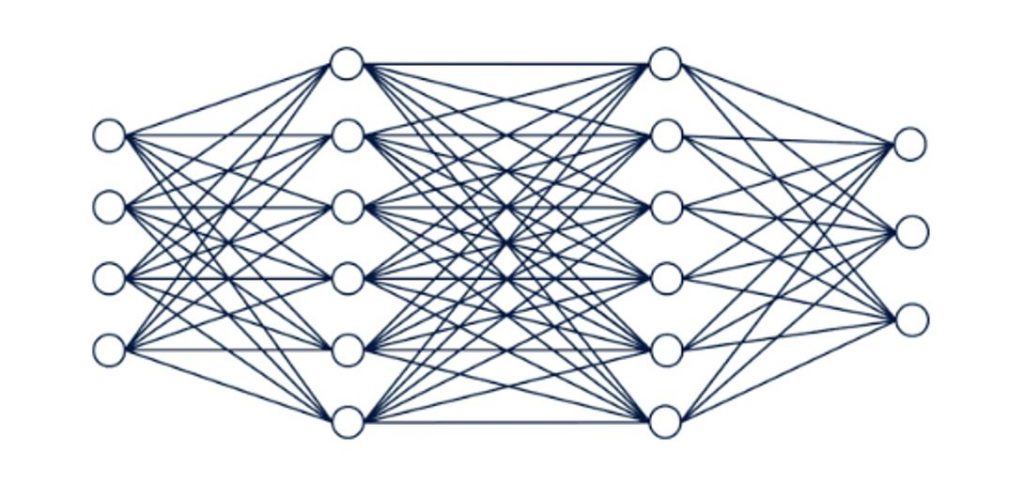
کلیت فرآیند شبکه عصبی در قالب ۴ گام مطرح می شود:
۱- مقداردهی اولیه وزن ها و بایاس ها
در ادامه در این مورد توضیح خواهیم داد.
۲- پیش انتشار
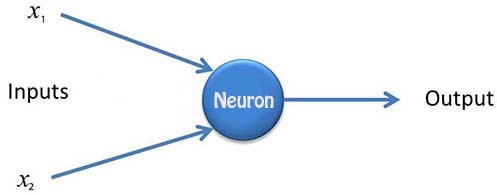
در پیش انتشار ورودی X به عنوان ورودی هر نرون مطرح می شود و هر نرون دو تابع را محاسبه می کند. یکی تابع خطی حاصل ضرب یعنی Z = W*X + b ، بوسیله وزن ها، ورودی ها و بایاس ها، وزن ها و ورودی را درهم ضرب می کنیم و بایاس را اضافه خواهیم کرد و سپس مجموع یابی را اجرا کرده و پس از گذشتن از این بخش به تابع فعال سازی می رسیم. تابع دوم، تابع فعال سازی (a = relu (z، که می توان از تابع های فعالسازی مختلفی استفاده نمود. این پروسه برای همه نرون ها ادامه می یابد و و ازمیان همه لایه ها حرکتی رو به جلو انجام می دهد و در نهایت به y_hat ( خروجی ) پیشبینی شده شبکه عصبی دست پیدا خواهیم کرد. با مقایسه این مقدار با مقدار واقعی، میزان خطا بدست میآید. این فرآیند پیش انتشار نامیده می شود.
۳- محاسبه تابع هزینه
تفاوت بین y_hat پیشبینی شده ( خروجی شبکه ) و مقدار واقعی y ، میزان هزینه و ازدست رفت نامیده می شود. این موضوع نشان می دهد پیشبینی های ما تا چه میزانی با هدف اصلی تفاوت دارد. هدف اصلی ما، به حداقل رساندن تابع هزینه است.
۴- پس انتشار
پس انتشار تکنیکی برای کاهش هزینه ( خطا ) می باشد (o/p پیشبینی شده – o/p واقعی). الگوریتم پس انتشار با مقایسه مقدار واقعی خروجی بدست آمده از فرآیند پیش انتشار، با مقدار مورد انتظار، آغاز می شود . سپس حرکتی رو به عقب در شبکه انجام می شود و هریک از وزن ها در مسیر کاهش میزان خطا، تنظیم می شود. در اینجا، درواقع مقدار بایاس ها را محاسبه، و وزن ها را با توجه به تابع هزینه بروز رسانی می کنیم. بروز رسانی وزن ها را تا دستیابی به میزان حداقل هزینه و ازدست رفت اجرا خواهیم کرد. هر دوی پیش انتشار و پس انتشار هزاران بار روی هر ترکیب ورودی اجرا می شود تا زمانی که شبکه بتواند بوسیله پیش انتشار، خروجی موردانتظار ورودی های مدنظر را با دقت کامل محاسبه کند.
گام های ۲ تا ۴ برای n بار تکرار می شود تا به میزان حداقل شده هزینه دست یابیم.
با مشاهده فرآیند شبکه عصبی می توانیم به سادگی بگوییم که گام های ۲، ۳ و ۴ ازنظر کارایی، برای هر شبک های یکسان عمل می کنند، درواقع عملیاتی مشابه انجام می دهند تا شبکه به سمت حداقل هزینه و خطا همگرایی پید اکند، تنها تفاوت بزرگ و تعیین کننده برای سرعت بخشیدن به این همگرایی، مقداردهی اولیه درست و مناسب برای وزن ها می باشد.
حال اجازه دهید انواع مختلف مقدار دهی اولیه وزن ها را مشاهده کنیم. قبل از ورود به این مضوع، شما را با چند اصطلاح علمی آشنا می کنیم.
Fan-in:
Fan-in تعداد ورودی های نرون می باشد.
Fan-out:
Fan-out تعداد خروجی های نرون است.
توزیع یکنواخت :
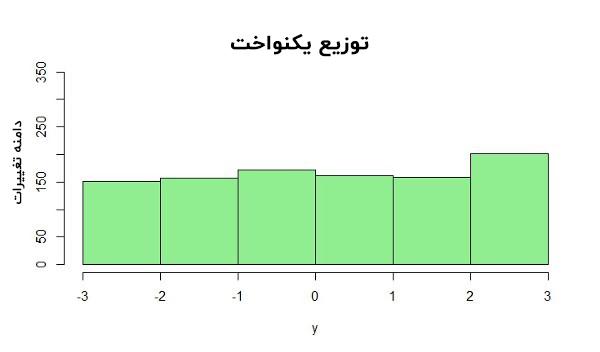
توزیع یکنواخت یک نوع از توزیع احتمالی است که تمام خروجیها بهطور مشابه برابرند، بهطور خاص احتمال درنظر گرفتهشدن هر متغیر به عنوان خروجی و نتیجه، با دیگر متغیرها یکسان است.
توزیع یکنواخت یک نوع از توزیع احتمالی است که تمام خروجی ها به طور مشابه برابرند، به طور خاص احتمال درنظر گرفته شدن هر متغیر به عنوان خروجی و نتیجه، با دیگر متغیرها یکسان است.
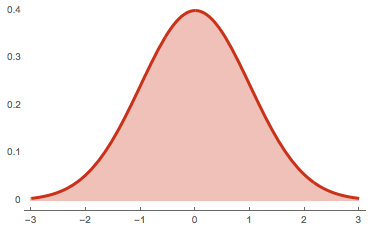
توزیع نرمال :
نگاهی اجمالی به مجموعه داده MNIST
مجموعه داده MNIST یکی از رایج ترین مجموعه داده های مورد استفاده برای دسته بندی تصویر می باشد. این مجموعه داده شامل تصاویر اعداد نوشته شده بوسیله دست می باشد و ما باید آن ها را به هر یک از ۱۰ کلاس مد نظر ( یعنی ۰-۹ ) دسته بندی کنیم.

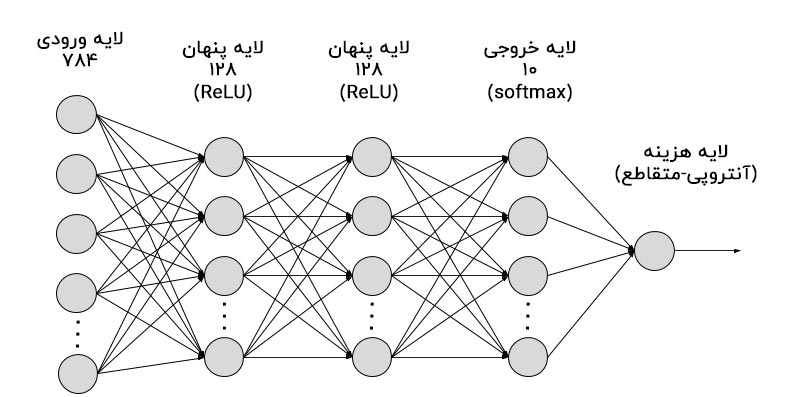
برای سادگی در نمایش ، ما فقط یک شبکه عصبی ۲ لای های را درنظر می گیریم، یعنی لایه پنهان ۱ با ۱۲۸ نرون و لایه پنهان ۲ با ۶۴ نرون. همچنین برای دسته بندی خروجی ها از دسته بند Softmax استفاده خواهیم کرد. در اینجا از ReLU به عنوان تابع فعال سازی استفاده می شود. خیلی خب بریم شروع کنیم.
مقداردهی اولیه صفر برای تمام وزن ها
فرضیه
در ابتدا مقدار صفر به وزن ها نسبت داده می شود. سپس تمام نرون ها در تمام لایه ها محاسبات یکسانی را اجرا می کنند و خروجی مشابه حاصل می کنند. خروجی بدست آمده باتوجه به تابع هزینه برای هر وزنی مشابه است و درنتیجه مدل چیزی یاد نخواهد گرفت و وزن ها بروزرسانی نخواهد شد. در اینجا ما با مسئله محو شدگی گرادیان مواجه هستیم که برای طولانی نشدن موضوع، از توضیح این مسئله دراین تحقیق خودداری می کنیم.
کدی برای تخصیص مقداراولیه صفر به وزن ها
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='zeros'))
model.add(Dense(64, activation='relu', kernel_initializer='zeros'))
model.add(Dense(output_dim, activation='softmax'))
خروجی بدست آمده از این نوع مقداردهی اولیه برای مجموعه داده MNIST
Epoch 1/5 60000/60000 [==============================] - 3s 55us/step - loss: 2.3016 - acc: 0.1119 - val_loss: 2.3011 - val_acc: 0.1135
Epoch 2/5 60000/60000 [==============================] - 3s 47us/step - loss: 2.3013 - acc: 0.1124 - val_loss: 2.3010 - val_acc: 0.1135
Epoch 3/5 60000/60000 [==============================] - 3s 46us/step - loss: 2.3013 - acc: 0.1124 - val_loss: 2.3010 - val_acc: 0.1135
Epoch 4/5 60000/60000 [==============================] - 3s 47us/step - loss: 2.3013 - acc: 0.1124 - val_loss: 2.3010 - val_acc: 0.1135
Epoch 5/5 60000/60000 [==============================] - 3s 46us/step - loss: 2.3013 - acc: 0.1124 - val_loss: 2.3010 - val_acc: 0.1135
نمودار مقادیر خروجی برای مقداردهی اولیه صفربه وزن ها
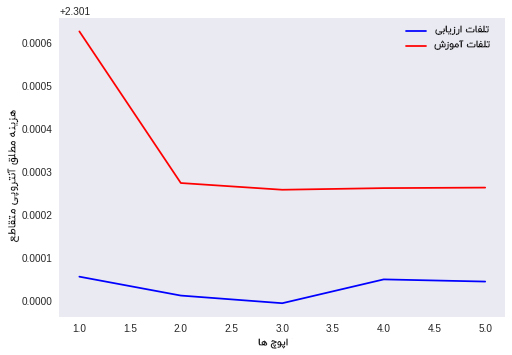
تجزیه و تحلیل خروجی
در این قسمت هزینه و درواقع میزان خطای آموزش و آزمایش تغییر پذیر نیست. بنابراین، ما می توانیم به سادگی نتیجه بگیریم وزن های نسبت داده شده تغییری نپذیرفته اند. از این موضوع درمیابیم که مدل ما تحت تأثیر مسئله محو شدگی گرادیان قرارگرفته است.
مقداردهی اولیه وزن ها بطور تصادفی
فرضیه
بجای انتساب مقداراولیه صفر به همه وزن ها، تمام وزن ها را با مقادیر تصادفی مقداردهی اولیه می کنیم. مقداردهی اولیه تصادفی بهتر از مقداردهی اولیه صفر به وزنه است. اما در مقداردهی اولیه تصادفی احتمال مواجه شدن با دو مسئله وجود دارد، یکی محو شدگی گرادیان و دیگری انفجار ( گسترش ) گرادیان ( Vanishing and Exploding gradient )، همانطور که پیشتر اشاره شد برای جلوگیری از ازدیاد مطلب، از توضیح این مسائل در این تحقیق خودداری کرده ایم. درواقع اگر به وزنه ا مقداراولیه بالایی تخصیص داده شود با مسئله انفجار گرادیان مواجه خواهیم شد. و همچنین اگر مقدار اولیه وزن ها خیلی پایین و کم باشد با مسئله محو شدگی گرادیان مواجه می شویم
کدی برای مقداردهی اولیه تصادفی وزن ها
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='random_uniform'))
model.add(Dense(64, activation='relu', kernel_initializer='random_uniform'))
model.add(Dense(output_dim, activation='softmax'))
خروجی بدست آمده از مقداردهی اولیه تصادفی وزن ها برای مجموعه داده MNIST
Epoch 1/5 60000/60000 [==============================] - 3s 55us/step - loss: 0.3929 - acc: 0.8887 - val_loss: 0.1889 - val_acc: 0.9432
Epoch 2/5 60000/60000 [==============================] - 3s 45us/step - loss: 0.1570 - acc: 0.9534 - val_loss: 0.1247 - val_acc: 0.9622
Epoch 3/5 60000/60000 [==============================] - 3s 53us/step - loss: 0.1069 - acc: 0.9685 - val_loss: 0.0994 - val_acc: 0.9705
Epoch 4/5 60000/60000 [==============================] - 3s 54us/step - loss: 0.0810 - acc: 0.9761 - val_loss: 0.0986 - val_acc: 0.9710
Epoch 5/5 60000/60000 [==============================] - 3s 54us/step - loss: 0.0629 - acc: 0.9804 - val_loss: 0.0877 - val_acc: 0.9755
نمودار مقادیر خروجی حاصل از مقداردهی اولیه تصادفی
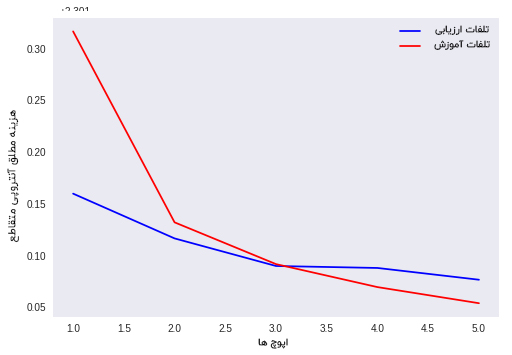
تجزیه و تحلیل خروجی
در این نوع مقداردهی اولیه، هزینه ( تلفات ) آموزش و آزمایش دچار تغییرات زیادی می شود، درواقع آن ها به سوی مقدار حداقل و مینیمم هزینه و خطا همگرایی پیدا می کنند. بنابراین، به طور واضح می توان گفت که مقداردهی اولیه تصادفی بهتر از تخصیص مقداراولیه صفر به وزن ها عمل می کند. همچنین هربار که مدل را مجدداً راه اندازی می کنیم، نتایج متفاوتی دریافت می کنیم چراکه مقداردهی اولیه به وزن ها، تصادفی است.
ادامه مطلب : روش های مقدار دهی اولیه در شبکه های عصبی ( بخش دوم )
بیشتر بخوانید :
- پلاک خوان خودکار بدون پردازنده گرافیکی : ALPR Without GPU
- هوش مصنوعی مولد به دنبال «تقویت نقاط قوت انسان» است نه جایگزینی با آن
- ANPR یا LPR : تفاوت چیست؟
- هوش مصنوعی مولد تهدیدات جدیدی برای امنیت سایبری ایجاد می کند
- فناوری تشخیص پلاک خودرو چگونه جامعه را هوشمندتر می کند
Hackernoon Quora Rumelhart, D. Hinton, G. Williams, R. (1985). Learning internal representations by error propagation
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب





ممنون
همچنان پیگیر مطالب سایت تون خواهیم بود.