در قسمت قبل با اهمیت مقدار دهی اولیه وزن ها در شبکه های عصبی و اهمیت انجام آن آشنا شدیم. در این قسمت به آشنایی با روش های دیگر انجام مقدار دهی اولیه وزن ها می پردازیم.
مقاله مرتبط :
مدل Xavier Glorot برای مقداردهی اولیه وزن ها
این مدل یک تکنیک پیشرفته در مقداردهی اولیه وزن ها بشمار می رود. دو نوع مقداردهی اولیه در این مدل مطرح است. یکی مدل مقداردهی اولیه نرمالِ Xavier Glorot و دومی مدل مقداردهی اولیه یکنواختِ Xavier Glorot.
می دانیم در شبکه عصبی، وزن ها معمولاً بهطور تصادفی مقداردهی اولیه می شوند و این نوع مقداردهی اولیه نیازمند رعایت عدالت و تکرار فرآیند الگوریتم به تعداد دفعات زیاد جهت همگرایی به سمت حداقل خطا و دستیابی به ماتریس وزن ایده آل، می باشد. یکی از اقدا مها جهت کاهش میزان خطا، انتخاب مقداراولیه تصادفی وزنها با دقت بیشتر می باشد. مدل مقداردهی اولیه Xavier که به عنوان الگوریتم Xavier نیز شناخته می شود، اندازه و سایز شبکه ( تعداد نرون های ورودی و خروجی ) را به صورت معادله ای درمی آورد و به رعایت مسائل گفته شده می پردازد.
Xavier Glorot و Yoshua Bengio ارائه دهندگان این مدل از مقداردهی اولیه بوده اند که بهتر از مقداردهی اولیه تصادفی عمل می کند. این مدل نه تنها احتمال بروز مسائل مربوط به گرادیان را کاهش می دهد بلکه همگرایی به سوی میزان خطای حداقلی را نیز درزمان کمتری ممکن می سازد.
مقداردهی اولیه Xavier Glorot
مقداردهی اولیه یکنواختِ Xavier: دریافت هر وزن w ، از طریق یک توزیع یکنواخت تصادفی در بازه [-x,x] برای 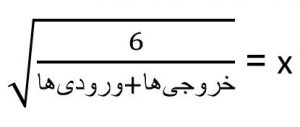
مقداردهی اولیه نرمالِ Xavier: دریافت هر وزن w ، از طریق یک توزیع نرمال با میانه ۰، و یک توزیع استاندارد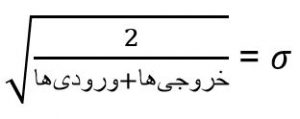
ایده اصلی: روش زیاد مهم نیست، تعداد ورودیها و خروجیهاست که مهم است.
الف) مقداردهی اولیه یکنواخت Xavier Glorot
دراین مدل وزن ها از طریق یک توزیع یکنواخت درون بازه +x و –x بدست می آیند که محدوده بازه براساس مقدار x برابر با مجذور ریشه یا ( (fan-in+fan-out)/6) sqrt، حاصل می شود.
کد مدل مقدارد دهی اولیه یکنواختِ Xavier Glorot
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='glorot_uniform'))
model.add(Dense(64, activation='relu', kernel_initializer='glorot_uniform'))
model.add(Dense(output_dim, activation='softmax'))
خروجی حاصل از مدل مقدارد دهی اولیه یکنواختِ Xavier Glorot
Epoch 1/5 60000/60000 [==============================] - 4s 68us/step - loss: 0.3317 - acc: 0.9072 - val_loss: 0.1534 - val_acc: 0.9545
Epoch 2/5 60000/60000 [==============================] - 3s 55us/step - loss: 0.1303 - acc: 0.9614 - val_loss: 0.1124 - val_acc: 0.9679
Epoch 3/5 60000/60000 [==============================] - 3s 54us/step - loss: 0.0889 - acc: 0.9731 - val_loss: 0.0978 - val_acc: 0.9711
Epoch 4/5 60000/60000 [==============================] - 3s 54us/step - loss: 0.0668 - acc: 0.9795 - val_loss: 0.0863 - val_acc: 0.9735
Epoch 5/5 60000/60000 [==============================] - 3s 55us/step - loss: 0.0529 - acc: 0.9840 - val_loss: 0.0755 - val_acc: 0.9771
مودار مدل Xavier Glorot از نوع مقدارد دهی اولیه یکنواخت وزن ها
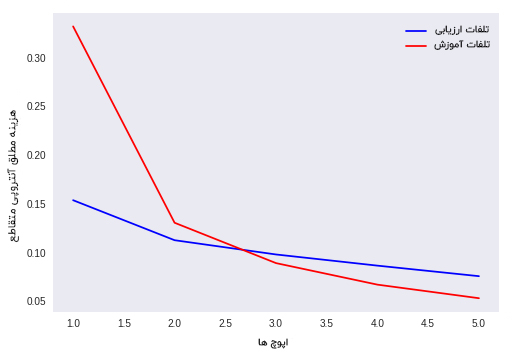
تجزیه و تحلیل خروجی
در این نوع مقداردهی اولیه یعنی مقداردهی اولیه یکنواختِ Xavier Glorot، مدل ما به سمت اجرایی بسیار خوب و کار آمد سوق پیدا می کند. همچنین اگر این مدل را چندین بار اجرا کنیم بازهم خروجی تغییری نمی پذیرد.
ب) مقداردهی اولیه نرمالِ Xavier Glorot
در این مدل وزن ها از طریق یک توزیع نرمال با میانه = ۰ و واریانس = مجذور ریشه یا ((fan-in+fan-out)/2) sqrt ،بدست می آید.
کد مدل مقدارددهی اولیه نرمالِ Xavier Glorot
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='glorot_normal'))
model.add(Dense(64, activation='relu', kernel_initializer='glorot_normal'))
model.add(Dense(output_dim, activation='softmax'))
خروجی حاصل از مدل مقدارددهی اولیه نرمالِ Xavier Glorot
Epoch 1/5 60000/60000 [==============================] - 4s 66us/step - loss: 0.3296 - acc: 0.9064 - val_loss: 0.1628 - val_acc: 0.9492
Epoch 2/5 60000/60000 [==============================] - 3s 50us/step - loss: 0.1359 - acc: 0.9597 - val_loss: 0.1119 - val_acc: 0.9658
Epoch 3/5 60000/60000 [==============================] - 3s 51us/step - loss: 0.0945 - acc: 0.9721 - val_loss: 0.0929 - val_acc: 0.9706
Epoch 4/5 60000/60000 [==============================] - 3s 52us/step - loss: 0.0731 - acc: 0.9776 - val_loss: 0.0804 - val_acc: 0.9741
Epoch 5/5 60000/60000 [==============================] - 3s 51us/step - loss: 0.0576 - acc: 0.9824 - val_loss: 0.0707 - val_acc: 0.9783
نمودار مدل Xavier Glorot از نوع مقدار دهی اولیه نرمال وزن ها

تجزیه و تحلیل خروجی
مشابه مدل یکنواختِ Xavier Glorot، در این نوع مقدار دهی اولیه یعنی مقدار دهی اولیه نرمالِ Xavier Glorot نیز مدل ما به سمت اجرا و کارایی بهتر سوق پیدامی کند و با چندین بار اجرا کردن الگوریتم، خروجی تغییر نخواهد کرد.
وزن هایی که در این مدل درنظر گرفته شده ، نه زیاد بزرگ است نه زیاد کوچک. بنابراین ما با مسئله محو شدگی ویا انفجار گرادیان ها مواجه نمی شویم. همچنین، مدل مقداردهی اولیه Xavier Glorot به همگرایی و دستیابی هرچه سریع تر به سوی میزان مینیمم خطا کمک بسیاری می کند.
مدل Heبرای مقداردهی اولیه وزن ها
این نوع از مقداردهی اولیه با عنوان hey تلفظ می شود و یک تکنیک پیشرفته در مقداردهی اولیه وزن ها به شمار می رود. تابع فعال سازی ReLU بوسیله این مدل مقداردهی اولیه، بسیار خوب عمل می کند. تنها پارامتری که در مقداردهی اولیه He درنظر گرفته می شود، تعداد ورودی هاست ( fan-in ). در مقداردهی اولیه He نیز مانند مدل Xavier، دو نوع از مقداردهی مطرح می شود، یکی مقداردهی اولیه نرمالِ He و دیگری مقداردهی اولیه یکنواختِ He.
الف) مقداردهی اولیه یکنواخت وزن ها He
در این مدل وزن ها بوسیله یک توزیع یکنواخت درون بازه +x و –x که x = مجذورریشه یا ( (fan-in)/6) sqrt است، بدست می آید.
کد مدل مقداردهی اولیه یکنواخت وزن ها He
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='he_uniform'))
model.add(Dense(64, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(output_dim, activation='softmax'))
خروجی حاصل از مدل مقداردهی اولیه یکنواخت وزن ها He
Epoch 1/5 60000/60000 [==============================] - 4s 72us/step - loss: 0.3252 - acc: 0.9050 - val_loss: 0.1524 - val_acc: 0.9546
Epoch 2/5 60000/60000 [==============================] - 3s 52us/step - loss: 0.1314 - acc: 0.9611 - val_loss: 0.1104 - val_acc: 0.9671
Epoch 3/5 60000/60000 [==============================] - 3s 54us/step - loss: 0.0928 - acc: 0.9718 - val_loss: 0.0978 - val_acc: 0.9697
Epoch 4/5 60000/60000 [==============================] - 3s 53us/step - loss: 0.0703 - acc: 0.9786 - val_loss: 0.0890 - val_acc: 0.9740
Epoch 5/5 60000/60000 [==============================] - 3s 53us/step - loss: 0.0546 - acc: 0.9828 - val_loss: 0.0860 - val_acc: 0.9740
نمودار مدل مقداردهی اولیه یکنواخت وزن ها He
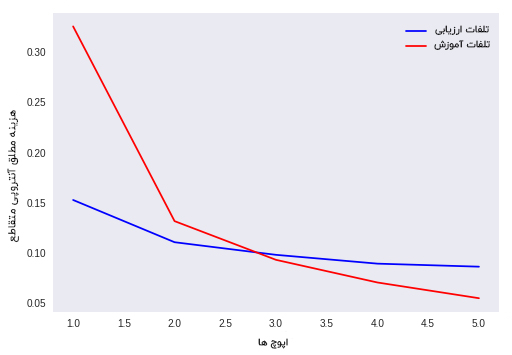
تجزیه و تحلیل خروجی
در این نوع مقداردهی اولیه یعنی مقدار دهی اولیه یکنواخت وزن ها He، فقط از تعداد ورودی ها استفاده می شود و به همین دلیل این مدل از مقداردهی اولیه اجرا و کارایی کاملاً رو به افتی خواهد داشت.
ب) مقداردهی اولیه نرمال وزن ها He
در این نوع از مقداردهی اولیه، وزن ها از طریق یک توزیع نرمال با میانه = ۰ و واریانس = مجذور ریشه یا ( (fan-in)/2) sqrt بدست می آید.
کد مدل مقداردهی اولیه نرمال وزن ها He
model = Sequential()
model.add(Dense(128, activation='relu', input_shape=(input_dim,), kernel_initializer='he_normal'))
model.add(Dense(64, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(output_dim, activation='softmax'))
خروجی حاصل از مدل مقداردهی اولیه نرمال وزن ها He
Epoch 1/5 60000/60000 [==============================] - 4s 61us/step - loss: 0.3163 - acc: 0.9087 - val_loss: 0.1596 - val_acc: 0.9508
Epoch 2/5 60000/60000 [==============================] - 3s 45us/step - loss: 0.1319 - acc: 0.9610 - val_loss: 0.1163 - val_acc: 0.9625
Epoch 3/5 60000/60000 [==============================] - 3s 44us/step - loss: 0.0915 - acc: 0.9725 - val_loss: 0.0897 - val_acc: 0.9727
Epoch 4/5 60000/60000 [==============================] - 3s 45us/step - loss: 0.0693 - acc: 0.9795 - val_loss: 0.0878 - val_acc: 0.9735
Epoch 5/5 60000/60000 [==============================] - 3s 44us/step - loss: 0.0537 - acc: 0.9836 - val_loss: 0.0764 - val_acc: 0.9769
نمودار مدل مقداردهی اولیه نرمال وزن ها He
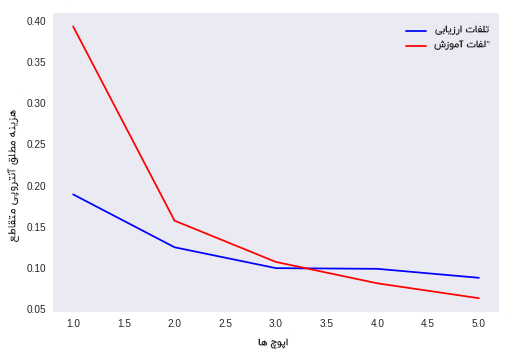
تجزیه و تحلیل خروجی
در این مدل یعنی مقداردهی اولیه نرمال وزن ها He، فقط از پارامتر تعداد ورودی ها استفاده می شود، اما برخلاف مدل مقداردهی اولیه یکنواخت وزن ها He، فقط بوسیله استفاده از تعداد ورودی ها نیز، مدل مد نظر کارایی خوبی خواهد داشت.
همچنین در مقداردهی اولیه He، وزن ها را نه زیاد بزرگ و نه زیاد کوچک درنظر می گیریم. بنابراین با مسائل محو شدگی و انفجار گرادیان ها مواجه نمی شویم. همچنین، مقداردهی اولیه He بطور مشابه با مدل مقداردهی اولیه Xavier Glorot، به همگرایی و دستیابی هرچه سریعتر به میزان مینیمم خطا کمک بسیاری می کند.
چگونه مقدار اولی های مناسب برای وزن ها انتخاب کنیم؟
از آنجایی که نظری های قوی درمورد انتخاب مقداراولیه مناسب برای وزن ها وجود ندارد، ما فقط چند قاعده و قانون از روش های مطرح شده را بررسی می کنیم:
- زمانی که تابع فعالسازی پیچیده باشد، بهتر است که از مدل Xavier Glorot برای مقداردهی اولیه وزن ها استفاده کنیم.
- وقتی تابع فعالسازی ReLU مد نظر است، بهتر است که از مدل مقدار دهی اولیه وزن ها He استفاده کنیم.
- در اکثر موارد در شبکه عصبی کانولوشن از تابع فعالسازی ReLU استفاده می شود و آن نیز طبق قاعده مطرح شده، از مدل مقداردهی اولیه He استفاده می کند.
بیشتر بخوانید :
- پلاک خوان های شهر گرینزبوروی آمریکا فعلاً قرار نیست افزایش پیدا کنند
- فرماندار اوکلند از پلاک خوان ها حمایت می کند اما مخالفان در اثربخشی آن تردید دارند
- لبنان استفاده از پلاک خوان های خودکار را تایید کرد
- چالش های مدیریت کلاس با ابزار جدید تشخیص چهره هوش مصنوعی
- آیا می توان از دوربین های ترافیکی برای گرفتن رانندگان الکلی استفاده کرد؟
Hackernoon Quora Rumelhart, D. Hinton, G. Williams, R. (1985). Learning internal representations by error propagation
 مجله هوش مصنوعی شهاب
مجله هوش مصنوعی شهاب






دم شما گرم